题目描述

在日本某处的一个动物园里，饲养员们决定和水豚们玩以下游戏。

水豚的围栏由 $N$ 个温泉组成，编号从 $0$ 到 $N-1$。这些温泉由 $N-1$ 条走道连接。每条走道连接两个温泉，并且可以从任何一个温泉通过这些走道到达任何其他温泉。换句话说，水豚围栏的结构是一棵树（即一个无向连通无环图）。

最初，每个温泉中最多只有一只水豚，但这在游戏过程中可能会改变。

游戏包含数轮（可能是无限轮）。每轮有两个阶段：

1. 饲养员会将一个橘子扔进 $N$ 个温泉中的一个。水豚们会知道橘子被扔进了哪个温泉。
2. 最多一只水豚可以移动到相邻的温泉。之后，如果装有橘子的温泉里没有水豚，则饲养员获胜，水豚失败。否则，橘子被吃掉，游戏继续。

一个初始配置（即最初包含水豚的温泉集合）是安全的，如果当饲养员和水豚都采取最优策略时，饲养员无法在有限轮内获胜。

对于从 $0$ 到 $N$ 的每个 $K$，找出恰好有 $K$ 只水豚的安全初始配置的数量。由于这些数字可能非常大，请找出它们对 $998244353$ 取模的余数。

实现细节

你将需要实现以下函数：

std::vector<int> solve(int N, std::vector<int> U, std::vector<int> V)

该函数由评分器调用一次，并应返回一个长度为 $N+1$ 的 std::vector<int>，其中包含对于每个 $0 \le K \le N$，恰好有 $K$ 只水豚的安全初始配置的数量（对 $998244353$ 取模）。

此函数的参数具有以下含义：

• $N$ - 温泉的数量。
• $U$ - 一个长度为 $N-1$ 的 std::vector<int>，包含 $N-1$ 条走道中每条的第一个端点。
• $V$ - 一个长度为 $N-1$ 的 std::vector<int>，包含 $N-1$ 条走道中每条的第二个端点。

对于每个 $0 \le i < N-1$，第 $i$ 条走道连接温泉 $U_i$ 和 $V_i$。

输入格式

见「实现细节」。

输出格式

见「实现细节」。

1

0 1

4 
0 1
1 2
2 3

0 0 4 4 1

6
0 1
1 2
1 3
0 4
4 5

0 0 0 0 11 6 1

15 
0 1
0 2
2 3
3 4
4 5
5 6
0 7
7 8
8 9
9 10
8 11
11 12
7 13
7 14

0 0 0 0 0 0 0 0 0 560 992 793 361 98 15 1

提示

样例解释

样例一解释

唯一的安全初始配置是 $\{0\}$。

样例二解释

第二个示例中水豚围栏的结构：

有 $4$ 个包含两只水豚的安全初始配置：$\{0, 2\}, \{0, 3\}, \{1, 2\}, \{1, 3\}$。

所有至少有 $3$ 只水豚的初始配置都是安全的。

样例三解释

第三个样例中水豚围栏的结构：

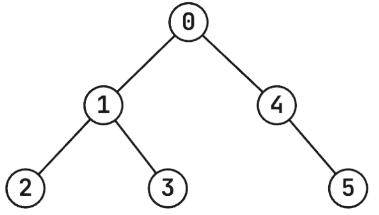
例如，初始配置 $\{1, 3, 4\}$ 是不安全的：

在第一轮中，饲养员会向温泉 5 中扔一个橙子。来自温泉 4 的水豚被迫移动到温泉 5。

在第二轮中，饲养员会向温泉 2 中扔一个橙子。来自温泉 1 的水豚被迫移动到温泉 2。

在第三轮中，饲养员会向温泉 0 中扔一个橙子。由于没有水豚可以移动到温泉 0，饲养员获胜。

样例四解释

第四个示例中水豚围栏的结构：

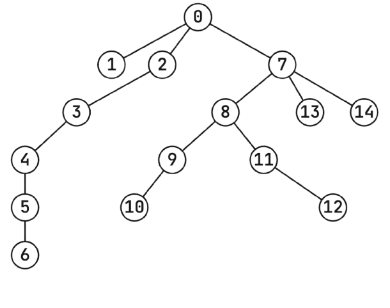
约束

• $1 \le N \le 6000$
• 对于每条走道 $(U_i, V_i)$，有 $0 \le U_i, V_i < N, U_i \ne V_i$
• 保证给定的走道构成一棵树（即一个无向连通无环图）。

#	得分	约束
$1$	$4$	存在一个温泉与其他所有温泉都直接相连。
$2$	$11$	每个温泉最多与其他两个温泉直接相连。
$3$	$14$	$N \le 10$
$4$	$9$	$N \le 20$
$5$	$33$	$N \le 200$
$6$	$29$	无额外限制