题目描述

It is well known that two disks on a plane have four distinct common tangent lines when they are disjoint (neither overlapping nor touching).

:::align{center} :::

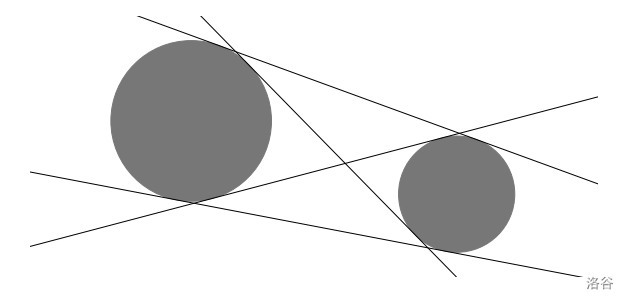You are given four lines on the $xy$-plane. Your objective is to apply parallel translations to these lines so that they become four distinct common tangent lines of some pair of disjoint disks with positive radii. You want to do this with a $cost$ as low as possible, where the cost is defined as the sum of the translation distances. The translation distance for a line is the distance between the lines before and after the translation.

Each line is specified by two parameters, $a$ and $d$, and is defined by

$$x \cos\left(\frac{\pi a}{180}\right) + y \sin\left(\frac{\pi a}{180}\right) = d.$$

For example, the line with $(a, d) = (60, 1)$ represents $x/2 + \sqrt{3}y/2 = 1$, since $\cos(\pi/3) = 1/2$ and $\sin(\pi/3) = \sqrt{3}/2$.

First, determine whether the objective is achievable. If it is, determine the minimum required cost, defined as follows: the minimum value $c$ such that the objective is achievable with a cost at most $c + \varepsilon$ for any positive real $\varepsilon$. The objective does not have to be achievable with the cost exactly equal to $c$.

输入格式

The input contains one or more test cases. The first line of the input contains an integer $t$ ($1 \le t \le 1000$), which is the number of test cases. The descriptions of the $t$ test cases follow, each in the following format.

$$a_1\ d_1$$ $$\vdots$$ $$a_4\ d_4$$

For $i = 1, \ldots, 4$, two integers $a_i$ and $d_i$ are the parameters that specify the $i$-th line ($0 \le a_i < 180$, $-1000 \le d_i \le 1000$). Two or more lines may be identical before translations.

输出格式

For each test case, if the objective is not achievable, output $no$ in a line. Otherwise, output the minimum required cost described above in a line. The absolute or relative error of the output must be less than or equal to $10^{-7}$.

4
90 0
90 0
45 0
135 0
0 -200
0 100
30 0
150 0
120 100
120 75
30 50
30 -100
178 -132
144 -83
165 199
19 31

0
86.602540378444
no
173.814220263386

提示

In the first test case of Sample Input 1, you have to move at least one of the first two identical lines (Figure L.1 (a)). For $\varepsilon > 0$, translating one line by $\varepsilon/2$ in the positive $y$-direction and the other by $\varepsilon/2$ in the negative $y$-direction achieves the objective with cost $\varepsilon$. This results in four tangent lines for disks with radii $\varepsilon/2$ (Figure L.1 (b)). Since $\varepsilon$ can be arbitrarily small, the minimum required cost is $0$. The remaining cases are illustrated in Figures L.1 (c) to (e).

:::align{center}

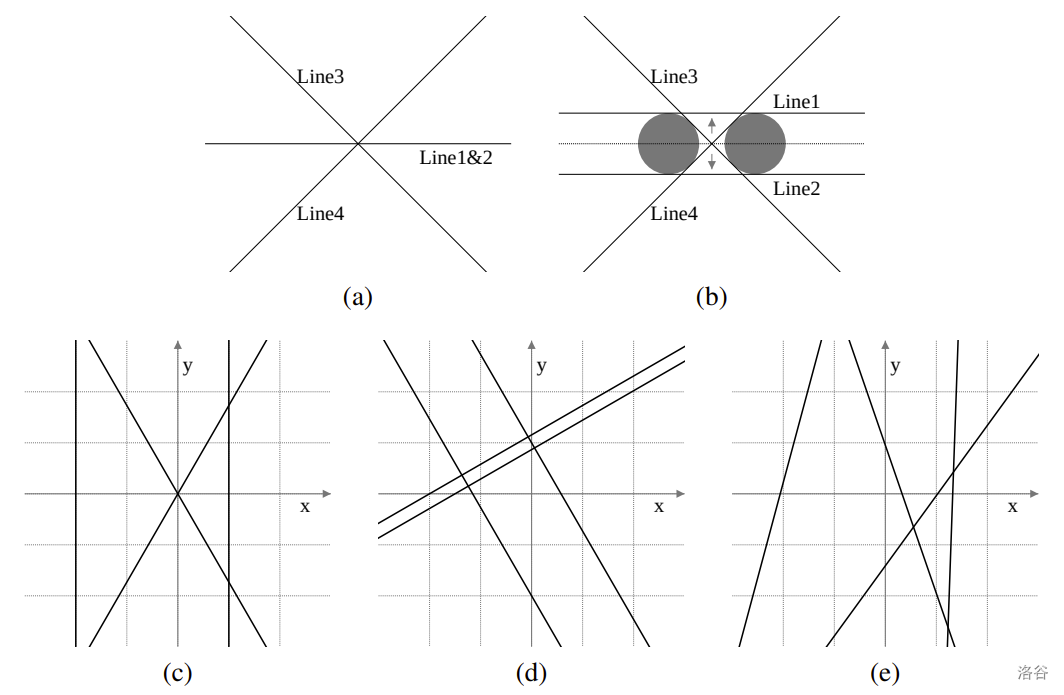
Figure L.1. Illustration of Sample Input 1 :::