题目描述

You, a young astronomer, are interested in the spatial arrangement of a set of stars with distinctive features. Knowing this might contribute to the understanding of early-universe cosmology. You can perform measurements using a specialized instrument for this purpose.

The instrument uses its own three-dimensional Cartesian coordinate system, in which the origin $(0, 0, 0)$ is set on Earth, and the positions of the stars are modeled as lattice points (points whose coordinates are all integers). You already know the distances to all the stars of interest from Earth, but their directions are unknown.

In a single measurement, you specify two distinct stars, and the instrument reports the distance between them. Note that the instrument does not report the absolute or relative directions of the stars.

Determine the distances between all pairs of the stars within the limited number of measurements.

Interaction

The first line of input contains an integer $n$, the number of stars of interest ($2 \le n \le 100$). The stars are numbered from 1 to $n$. The second line contains $n$ integers. The $i$-th of them is the squared distance from the origin to star $i$. It is guaranteed that all stars have integer coordinates, each between $-4000$ and $4000$, inclusive. No two stars are at the same position. No star is at the origin.

After reading in these two lines, you may start measurements. To measure the distance between stars $i$ and $j$, write a line of the form "measure $i$ $j$", where $i$ and $j$ are distinct integers between 1 and $n$, inclusive. In response, an input line containing an integer denoting the squared distance between stars $i$ and $j$ becomes available. You can perform up to $300$ measurements.

When you have determined the distances between all pairs of the stars, write a line containing only answer, followed by $n-1$ lines of the following format.

$$d_{1,2}\ d_{1,3}\ \cdots\ d_{1,n}$$ $$d_{2,3}\ \cdots\ d_{2,n}$$ $$\vdots$$ $$d_{n-1,n}$$

Here, $d_{i,j}$ ($1 \le i < j \le n$) is an integer denoting the squared distance between stars $i$ and $j$. Note that you do not need to determine the stars' coordinates. After writing these lines, the interaction stops, and your program must terminate without any extra output.

If your output does not conform to the specifications above, or if the number of measurements exceeds $300$, your submission will be judged as a wrong answer.

The coordinates of the stars are fixed before the interaction starts; they do not change during the interaction.

You are provided with a command-line tool for local testing. For more details, refer to the clarifications in the contest system.

3
1 11 4

14

11

9

measure 1 2

measure 2 3

measure 3 1

answer
14 9
11

4
47944017 47920034 47960009 47968006

answer
191728099 2 191824043
191760077 12
191856029

5
1 4 9 50 149

answer
5 10 45 162
13 38 181
29 206
371

提示

In Sample Interaction 1, the stars' coordinates can be as follows:

• star 1 is at $(1, 0, 0)$,
• star 2 is at $(-1, -1, 3)$, and
• star 3 is at $(-2, 0, 0)$.

The distance between stars 1 and 2 is $\sqrt{14}$. In the first measurement, the squared distance, $14$, is returned.

:::align{center}

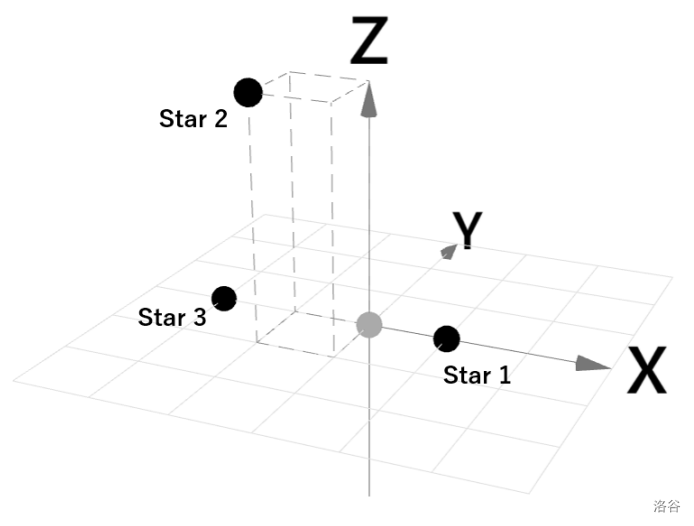
Figure F.1. Illustration of Sample Interaction 1 :::

In Sample Interaction 2, the stars' coordinates can be as follows:

• star 1 is at $(-3998, -3998, -3997)$,
• star 2 is at $(3997, 3997, 3996)$,
• star 3 is at $(-3999, -3998, -3998)$, and
• star 4 is at $(3999, 3999, 3998)$.

In Sample Interaction 3, the stars' coordinates can be as follows:

• star 1 is at $(1, 0, 0)$,
• star 2 is at $(0, -2, 0)$,
• star 3 is at $(0, 0, 3)$,
• star 4 is at $(3, -4, 5)$, and
• star 5 is at $(-6, 7, -8)$.