题目描述

You are preparing miso soup, a favorite among Japanese people, with one of the most popular ingredients, tofu. Tofu is a white cuboid-shaped food that is usually cut into smaller pieces and then put into the soup.

You plan to chop a single block of tofu to make at least a required number of cubes of the same size. You cut the tofu along planes parallel to the faces of the tofu block. Each cut goes all the way through the block, dividing all the pieces it passes through. You should not move the tofu block nor its fragments until tofu cubes are completely cut out.

:::align{center}

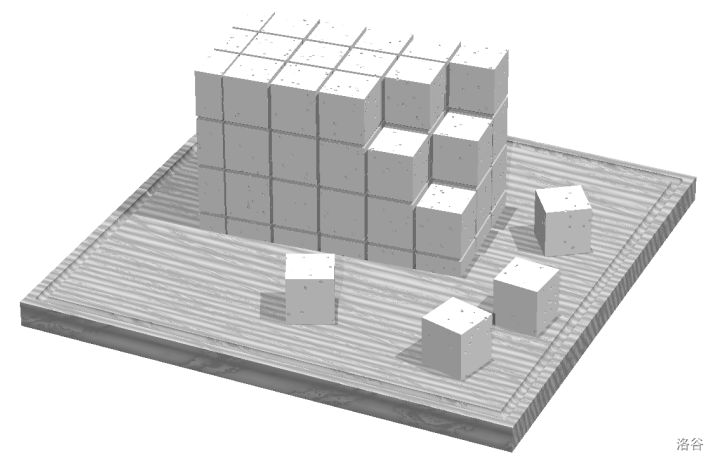
Figure E.1. An example of cutting the tofu :::

As long as the required number of tofu cubes can be obtained, you want to make cubes as large as possible. You don't mind leaving excess tofu cubes or leftover fragments, as they can be used for other dishes.

Given the dimensions of the block of tofu (its length, width, and height) in integer multiples of unit length, and the required number of tofu cubes, your task is to find the maximum possible side length of the tofu cubes. Since it can be proven that the answer is a rational number under the given constraints, it should be represented as a reduced fraction.

输入格式

The input contains one or more test cases. The first line of the input contains an integer $t$ ($1 \le t \le 10^4$), which is the number of test cases. The descriptions of the $t$ test cases follow, each in the following format.

The three integers $a$, $b$, and $c$ represent the length, width, and height of the block of tofu, respectively. They are between 1 and $10^9$, inclusive. The integer $k$ ($1 \le k \le 10^9$) represents the required number of tofu cubes.

输出格式

For each test case, output two positive integers $p$ and $q$ in a line, separated by a single space. Here, $p$ and $q$ are mutually prime integers, meaning that $p/q$ is the maximum possible side length of the tofu cubes.

3
1 1 1
2
2 2 3
7
2 3 5
240

1 2
1 1
1 2

3
1000000000 999999998 999999999
1000000000
1 1 999999999
1000000000
314 1000000000 1000000000
271828

499999999 500
999999999 1000000000
314 1