题目描述

An island on an extrasolar planet is famous as a good bird-watching spot, where you can see many seagull-lookalikes (simply called seagulls hereafter) throughout a year. The planet is quite similar to the Earth, but the number of days in a year is different.

Each seagull comes to the island exactly once a year, stays for a while, and leaves exactly once a year as well. Each seagull has its own schedule of coming and leaving the island, and quite punctually sticks to the schedule. That is, every year, it comes to the island on the same day of the year. Also, every year, it leaves on the same day of the year. Seagulls come to the island early in the morning and leave late in the afternoon. Seagulls that have come to the island may leave on the same day. On the other hand, seagulls may leave the island on one day and come again on the next day.

Members of the bird-watching club count the number of seagulls staying on the island every day around noon. Their counting is perfect, so that all seagulls present at that time are counted without any omission or duplication. However, the seagulls look so similar that identifying individuals is not possible.

Note that seagulls that leave the island on one evening and come again on the next morning are counted on all days in a year.

Given the daily counts of seagulls throughout a year, you want to know the total number of seagulls visiting the island. Since seagulls are indistinguishable, it is not possible to know the exact number. For example, if the counts are one on two consecutive days, the number of seagulls may be one or two. The minimum possible number is the only valuable information you can obtain.

Determine the minimum possible number of individual seagulls counted at least once in a year. If this minimum is small enough, also show a possible list of their stay periods that attains this minimum.

输入格式

The input consists of a single test case of the following format.

$$n$$ $$b_1 \ b_2 \ \cdots \ b_n$$

The integer $n$ ($2 \le n \le 2 \times 10^5$) is the number of days in one year on that planet. Days are numbered from 1 to $n$ throughout a year. The integer $b_i$ ($0 \le b_i \le 2 \times 10^5$) is the number of seagulls counted on day $i$. At least one of $b_i$'s is non-zero.

输出格式

Output the minimum possible number $m$ of seagulls in the first line. If $m$ is not greater than $2 \times 10^5$, then output $m$ additional lines describing one possible list of their stay periods. The $j$-th of these $m$ lines should contain two integers $s_j$ and $t_j$ ($1 \le s_j \le n$, $1 \le t_j \le n$) separated by a space, representing that the $j$-th seagull comes to the island on day $s_j$ and leaves on day $t_j$. Note that $s_j$ may be greater than $t_j$. In this case, the seagull stays on the island across years, from the last day of a year to the first day of the following year. When there are two or more possibilities, any of them is acceptable.

7
1 0 1 2 2 0 1

3
3 5
4 5
7 1

2
1 1

1
1 2

6
1 2 1 2 2 1

2
2 5
4 2

4
200000 0 200000 0

400000

提示

The following figure depicts the visiting schedules of three seagulls in Sample Output 1. Note that the third seagull stays in the island across years.

:::align{center}

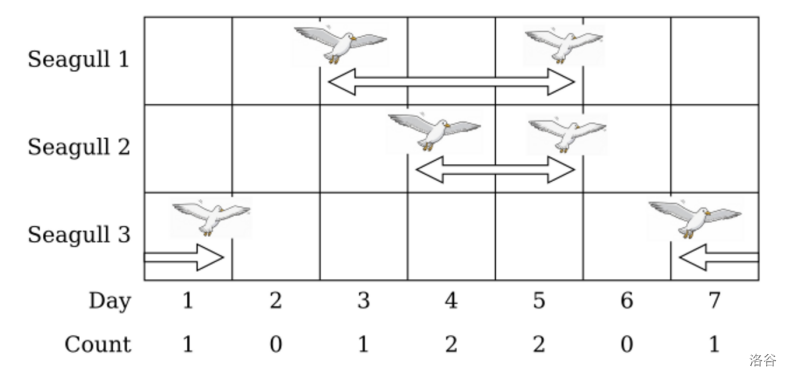
Figure C.1. Visiting schedules of the seagulls of Sample Output 1 :::