题目描述

In the first quadrant of a coordinate plane, you are given $n$ line segments parallel to the $x$-axis. Each segment $S_i$ ($1 \le i \le n$) is represented by the coordinates of its left and right endpoints, $(l_i, y_i)$ and $(r_i, y_i)$, respectively. All coordinates are positive integers.

You must now answer $q$ queries. For each query, a vertical line $x = p$, parallel to the $y$-axis, is given. The vertical line is represented by a single positive integer $p$.

If each segment $S_i$ is horizontally extended, it will eventually meet the line $x = p$ at the point $(p, y_i)$. If the segment, including its endpoints, already meets $x = p$, no extension is needed. For example, suppose there are 5 segments $\{(2,3), (5,3)\}$, $\{(4,6), (9,6)\}$, $\{(8,2), (12,2)\}$, $\{(11,4), (13,4)\}$, and $\{(14,5), (17,5)\}$, and a single line $x = 11$. The first segment must be extended by 6 to the right, the second segment 2 to the right, the third and the fourth segments 0, and the fifth segment 3 to the left for each to meet $x = 11$.

For each query, determine the maximum among the extension lengths required for all segments to meet the line $x = p$. Formally, let $\text{dist}(p, S_i)$ denote the distance that segment $S_i$ must be extended to intersect $x = p$ at $(p, y_i)$. For each query, output $\max_{1 \le i \le n} \text{dist}(p, S_i)$. In the example above, the answer to the query is 6. See the figure below.

:::align{center} :::

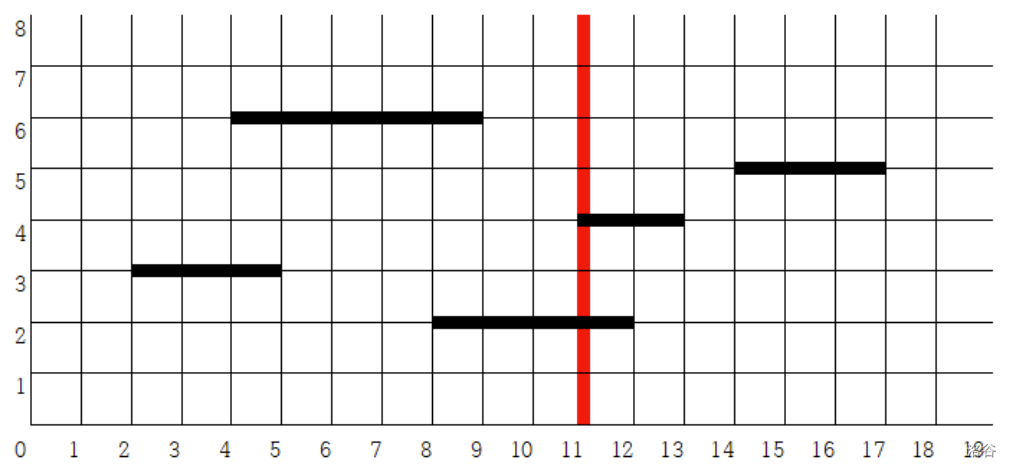Given $n$ segments and $q$ queries, write a program to output the maximum extension length for each query.

输入格式

Your program is to read from standard input. The input starts with a line containing two integers $n$ ($1 \le n \le 2 \times 10^6$) and $q$ ($1 \le q \le 2 \times 10^6$), where $n$ is the number of line segments and $q$ is the number of queries. In the following $n$ lines, the $i$-th line contains three integers, $l_i$, $r_i$, and $y_i$ ($1 \le l_i \le r_i \le 10^9$, $1 \le y_i \le 10^3$), where $l_i$ (resp. $r_i$) is the $x$-coordinate of left (resp. right) endpoint of $S_i$ and $y_i$ is the $y$-coordinate of both endpoints of $S_i$. In the following $q$ lines of queries, the $j$-th line contains one integer $p_j$ ($1 \le p_j \le 10^9$) which denotes the vertical line $x = p_j$.

输出格式

Your program is to write to standard output. Print exactly one line per each query. The $j$-th line should contain the maximum among the extension lengths required for all segments to meet $x = p_j$ at $(p_j, y_j)$.

5 3
2 5 3
4 9 6
8 12 2
11 13 4
14 17 5
11
5
1

6
9
13

4 8
1 4 7
3 7 5
10 13 8
12 15 2
13
7
4
8
3
11
1
16

9
5
8
4
9
7
11
12