题目描述

:::align{center} :::

The magic door to a treasure cave is an $m \times n$ grid filled with various gems. The gems fall into three categories: regular gems of various colors and shapes, and two special types - bomb gems and vibranium gems.

A match-3 group is a group of three or more identical regular gems aligned consecutively in a vertical or horizontal direction. A single gem may belong to both a horizontal match-3 group and a vertical match-3 group at which they intersect each other. Bomb gems do not form match-3 groups. Vibranium gems do not either.

In the initial state of the grid, no match-3 groups exist. When you initially touch two regular gems with your hand, they swap their positions. This single swap triggers a chain reaction that causes the gems to disappear from the grid according to a set of specific rules.

After the initial swap, the following process repeats until no more changes occur on the grid:

• Stage 1: Chain Reactions of Match-3 Groups

  1. All gems belong to every match-3 group disappear simultaneously.
  2. All types of gems above the vanished gems fall downward due to gravity, filling the empty spaces. During this process, any bomb gem that moves down by at least one cell becomes activated.
  3. If new match-3 groups are formed after the gems fall, this stage repeats from the first sub-step.
  4. If no more match-3 groups are formed, proceed to Stage 2.

• Stage 2: Activated Bomb Detonation

  1. All bombs currently in the activated state explode simultaneously.
  2. Each exploding bomb emits beams in horizontal and vertical directions.
  3. The beams travel from the bomb's position to the grid edge.
  4. A beam's path is blocked if it hits a vibranium gem.
  5. All regular gems and bombs on the beam's path disappear along with the exploded bomb.
  6. Unexploded bombs hit by a beam simply disappear without exploding.
  7. The gems above the vanished gems fall downward due to gravity, filling the newly created empty spaces. During this process, any bomb that moves down by at least one cell becomes activated. Then Stage 1 repeats.

Once no more changes occur due to Stage 1 and Stage 2, the entire process is terminated. Note that bomb gems and vibranium gems are not selected from the initial swap and do not form match-3 groups. Also note that any vibranium gem never disappears, acts as a barrier blocking the bomb's beam, and it is affected by gravity and will fall into empty spaces below it.

For example, consider a magic door composed of a $6 \times 4$ grid, as shown in Figure 1. In the figure, $0$ represents a bomb gem, $-1$ represents a vibranium gem, and positive numbers represent regular gems. Starting from the initial state shown in the figure (a), swapping the two gems located at $(6,1)$ and $(5,4)$ results in the state shown in (b). The location $(r,c)$ denotes the cell in the $r$-th row from the top and the $c$-th column from the left. Coordinates are 1-based. This state contains a match-3 group consisting of three $2$s. According to Stage 1, when the gems in this group disappear, state (c) is reached. At this point, the bomb gem at $(4,3)$ is activated and a new match-3 group consisting of three $1$s is formed. Again, Stage 1 removes the three gems of $1$, resulting in state (d). Since no match-3 groups remain, the bomb explodes due to Stage 2. This results in state (e). Here, two match-3 groups consisting of three $1$s and four $3$s are formed. Again, when these gems disappear due to Stage 1, state (f) is reached. No further changes occur in this state, making it the final state. A total of $18$ gems disappear during this process.

:::align{center}

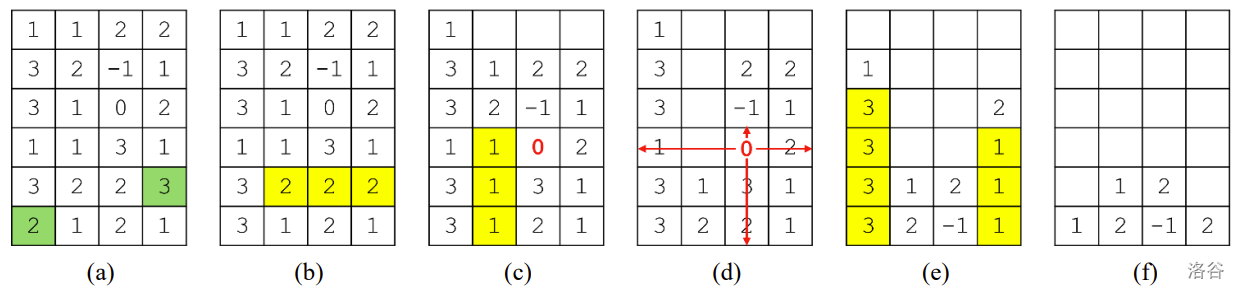
Figure 1. Chain Reactions :::

The magic door opens when a specific number of gems disappear. Your task is to write a program that, given the information about the magic door and the positions of the two regular gems to be swapped, calculates the number of gems that disappeared after the entire chain reaction, initiated by a single swap, comes to a complete stop.

输入格式

Your program is to read from standard input. The input starts with a line containing two integers, $m$ and $n$ ($3 \le m \le 80$; $3 \le n \le 80$), representing the number of rows and columns of the grid. The next $m$ lines each contain $n$ integers, representing the gems in each row of the grid, where $0$ represents a bomb gem, $-1$ represents a vibranium gem, and integers between $1$ and $9$ inclusive represent regular gems. The final line contains four integers, $r_1, c_1, r_2, c_2$ ($1 \le r_1, r_2 \le m$; $1 \le c_1, c_2 \le n$), where $(r_1, c_1)$ and $(r_2, c_2)$ represent the coordinates of the two distinct regular gems to be swapped. The coordinates are 1-based.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain an integer representing the total number of gems that will disappear after all processes have been completed.

6 4
1 1 2 2
3 2 -1 1
3 1 0 2
1 1 3 1
3 2 2 3
2 1 2 1
6 1 5 4

18

4 5
0 2 1 2 2
0 1 2 2 0
1 1 2 1 0
2 -1 -1 -1 2
3 3 3 4

15