题目描述

JOI 君正在使用一个纵向 3 格、横向 $N$ 格的矩形棋盘和若干棋子进行游戏。在游戏的初始状态下，至少有一个格子上放置了棋子，同时至少有一个格子上没有放置棋子。

该游戏的目标是：在尚未放置棋子的格子上逐个放置棋子，直到棋盘上所有格子都被放置棋子为止。但放置棋子需满足以下任一条件：

• 该格子正上方和正下方的格子上均已有棋子。
• 该格子左侧和右侧的格子上均已有棋子。

JOI 君从游戏的初始状态开始，对达成目标所需的放置顺序总数感到好奇。然而，这个数值可能非常巨大。

你的任务是：代替 JOI 君，求出从游戏初始状态开始到达成目标为止，所有可能的棋子放置顺序的数量，并对 $1\,000\,000\,007$ 取模。

题目

当给定游戏的初始状态时，请编写程序，求出从初始状态到达成目标为止所有可能的棋子放置顺序的数量对 $1\,000\,000\,007$ 取模的结果。

输入格式

从标准输入读取以下数据：

• 第 1 行包含一个整数 $N$，表示游戏所用棋盘的尺寸：纵向 3 格，横向 $N$ 格。
• 接下来的 3 行，每行包含一个长度为 $N$ 的字符串。每个字符为 ‘o’ 或 ‘x’。第 $i$ 行（$1 \le i \le 3$）从左往右第 $j$ 个字符（$1 \le j \le N$）表示棋盘第 $i$ 行、第 $j$ 列格子的初始状态。若该字符为 ‘o’，表示该游戏初始状态下该格子上已放置棋子；若为 ‘x’，则表示该游戏初始状态下该格子上未放置棋子。

输出格式

向标准输出输出一行，表示从初始状态到达成目标为止所有可能的棋子放置顺序的数量对 $1\,000\,000\,007$ 取模的结果。

3
oxo
xxo
oxo

14

10
ooxooxoxoo
xooxxxoxxx
oxoxoooooo

149022720

10
ooxoxxoxoo
oxxxxxoxxx
oxooxoxoxo

0

20
oxooxoxooxoxooxoxoxo
oxxxoxoxxxooxxxxxoox
oxooxoxooxooxooxoxoo

228518545

提示

样例 1 解释

游戏的初始状态如下图所示（用 ◯ 表示有棋子放置）：

:::align{center} :::

以下是所有可以从初始状态达到最终状态的方案，其中序号为放棋子的顺序，共有 $14$ 种方案：

:::align{center} :::

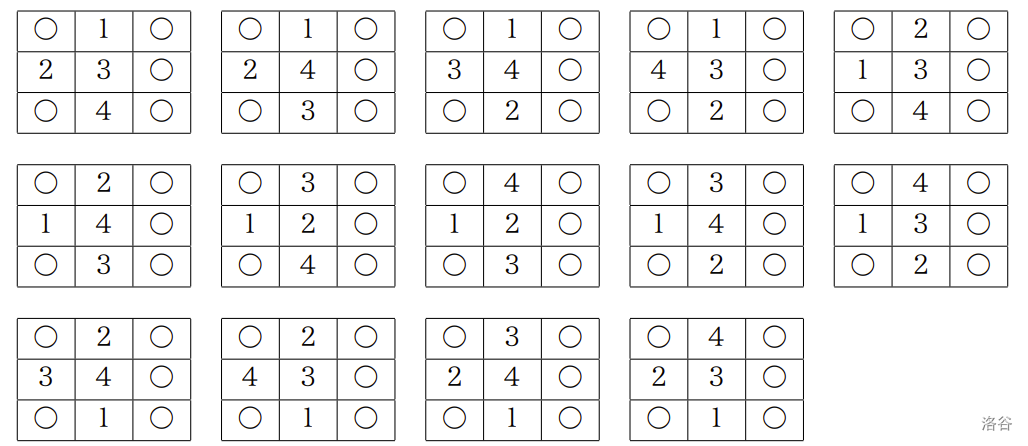数据范围

所有输入数据满足以下条件：

• $1 \le N \le 2000$。

子任务

子任务 1 [10 分]

满足以下条件：

• 游戏初始状态下，未放置棋子的格子数量不超过 16 个。
• $N \le 30$。

子任务 2 [12 分]

• 游戏初始状态下，对于每一个未放置棋子的格子，其上下左右四个相邻格子中，未放置棋子的格子数量不超过 2 个。

子任务 3 [20 分]

满足以下条件：

• 游戏初始状态下，不存在纵向连续 3 个格子均未放置棋子的情况。
• $N \le 30$。

子任务 4 [38 分]

• 满足 $N \le 300$。

子任务 5 [20 分]

无额外限制。

翻译由 Qwen3-235B 完成