题目描述

You are opening a cat cafe in Baku and would like to take a promotional photograph of all the cats sitting in the front window. Unfortunately, getting cats to do what you want is a famously hard problem. But you have a plan: you have bought a collection of $m$ catnip plants, each of a different variety, knowing that each cat likes some of these varieties. There is a row of $m$ pots in the window, numbered 1 to $m$ in order, and you will place one plant in each pot. Each cat will then be persuaded (by means of a toy on a string) to walk along the row of pots from 1 to $m$. As soon as a cat reaches a pot with a catnip plant that it likes, it will stop there, even if there already are other cats at that plant.

:::align{center}

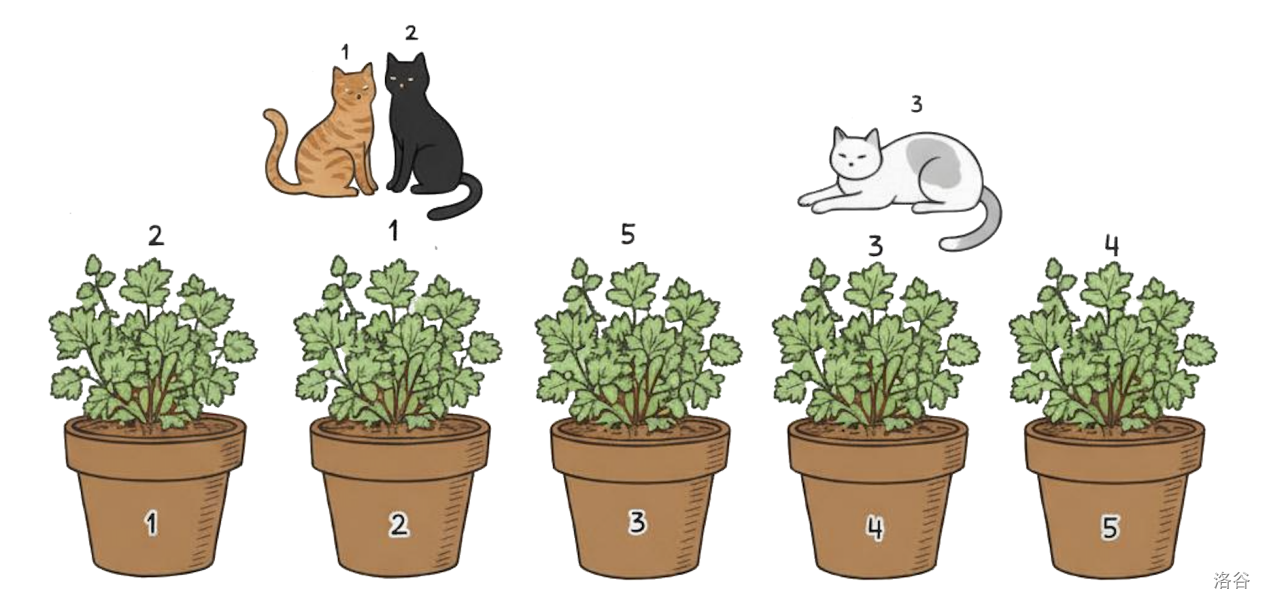
Figure F.1: One possible plant ordering for the first sample test case. :::

You know which pot you would like each cat to stop beside. Can you find a way in which to place the plants in the pots to achieve this?

输入格式

The first line of input contains an integer $t$ ($1 \le t \le 10\,000$), which is the number of test cases. The descriptions of $t$ test cases follow.

The first line of each test case contains two integers $n$ and $m$, where $n$ ($1 \le n \le 2 \cdot 10^5$) is the number of cats, and $m$ ($1 \le m \le 2 \cdot 10^5$) is the number of catnip plants (and also the number of pots). Catnip plants are numbered from 1 to $m$.

The following $n$ lines each describe one cat. The line starts with two integers $p$ and $k$, where $p$ ($1 \le p \le m$) is the pot at which the cat should stop, and $k$ ($1 \le k \le m$) is the number of catnip plants the cat likes. The remainder of the line contains $k$ distinct integers, which are the numbers of the plants that the cat likes.

Over all test cases, the sum of $n$ is at most $2 \cdot 10^5$, the sum of $m$ is at most $2 \cdot 10^5$, and the sum of all $k$ is at most $5 \cdot 10^5$.

输出格式

For each test case, output either yes if it is possible to arrange the catnip plants as described above, or no if not.

2
3 5
2 2 1 5
2 3 1 4 5
4 2 3 4
3 5
2 2 1 5
2 3 1 4 5
5 2 3 4

yes
no

提示

Explanation of Sample 1: In the first test case, a possible ordering of the plants is $[2, 1, 5, 3, 4]$. This way, cat 1 will stop at pot 2, as it is the first pot with a plant variety that it likes. Cat 2 will stop there as well. Cat 3 will continue all the way to pot 4, as shown in Figure F.1.