题目背景

译自 ROI 2014 Day1 T4. Коллайдер 2.0

题目描述

对撞机是一种用于研究基本粒子碰撞的装置。在其运行过程中，粒子被加速到极高速度。一个专门的探测器可以记录粒子的轨迹，这些轨迹在水平平面上表现为直线。

探测器的上方安装有一台超高速摄像机，其支架可以在水平平面上旋转。摄像机在任意时刻的方向由一条导向直线确定。摄像机可以拍摄任意矩形区域，并且该矩形的某一边必须与导向直线平行。

为了便于分析粒子可能发生的碰撞，要求每一张照片都必须包含截至拍摄时刻的所有轨迹交点。由于摄像机使用的耗材非常昂贵，因此每一张照片的面积必须尽可能小。

你的任务是：给定一系列按时间顺序发生的两类事件：

• 新的粒子轨迹出现；
• 摄像机按照指定导向直线拍摄一张照片；

对于每一张照片，求出包含所有轨迹交点的最小矩形区域的面积。

输入格式

第一行包含一个整数 $n$，表示事件总数（$1 \leqslant n \leqslant 200\,000$）。

接下来的 $n$ 行中，每行描述一个事件。

每个事件包含 5 个元素：

• 第一个元素为 +，表示出现一条新的轨迹；或为 ?，表示摄像机拍摄一张照片。
• 随后的 4 个元素为整数 $x_1$、$y_1$、$x_2$、$y_2$，表示两个不重合的点的坐标（$-10\,000 \leqslant x_1, y_1, x_2, y_2 \leqslant 10\,000$）。
• 对于 + 事件，这两个点位于该粒子轨迹上，且所有轨迹两两不同。对于 ? 事件，这两个点位于摄像机的导向直线上。

输出格式

设共有 $q$ 次拍摄事件。

输出 $q$ 个实数，分别表示每一张照片最小可能的矩形区域面积，输出顺序与拍摄顺序一致。

如果输出的面积为 $a$，标准答案为 $b$，则当满足以下条件时，该测试点被认为正确：

$$\frac{|a - b|}{\max(1, b)} \leqslant 10^{-4}.$$

6
+ 0 0 0 1
+ 0 0 1 0
+ 1 0 0 2
? 0 0 0 1
+ 2 4 3 6
? 0 0 1 1

2.0
3.000

7
? 11 4 -7 8
+ -2 -2 1 1
? 0 0 0 1
+ 0 1 1 0
+ 0 2 2 0
? 0 0 0 1
? 0 0 1 1

0.0
0.0
0.25
0.0000000

提示

样例 1 解释

:::align{center} :::

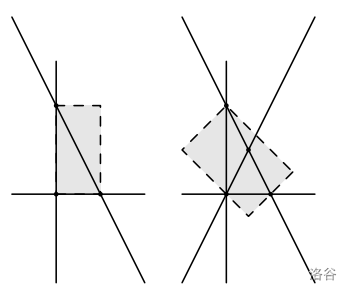样例 2 解释

:::align{center} :::

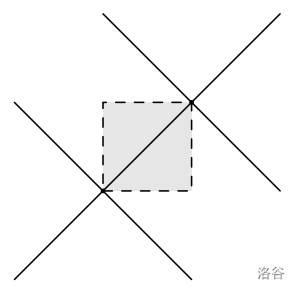数据范围

测试共 $50$ 组，独立计分，每组 $2$ 分。下表给出了部分测试的参数信息。

测试点	$n$	$q$	备注
$1$	$10$	$1$	引导直线平行于坐标轴
$2$	$20$	$10$
$3$	$745$	$365$
$4$	$1997$	$10$
$5$	$2000$	$1000$
$6$	$100001$	$1$
$7$	$100002$
$8$	$200000$
$9$		$100000$
$10$		$130000$
$11$	$1000$	$10$
$12$	$500$	$250$
$13$	$10100$	$10000$
$14$	$700$	$100$
$15$	$800$	$71$
$16$	$2001$	$1000$
$17$	$5003$	$2000$
$18$	$7005$	$4000$
$19$	$8007$	$1000$
$20$	$9009$	$4500$
$21$	$90100$	$90001$
$22$	$5000$	$101$
$23$	$6000$	$98$
$24$	$5432$	$2345$
$25$	$9508$	$4079$
$26$	$156002$	$151001$	所有照片拍摄在所有粒子出现之后
$27$	$157004$	$152001$
$28$	$197062$	$190001$
$29$	$148008$	$141001$
$30$	$169010$	$163501$
$31$	$165011$	$159001$
$32$	$185001$	$179102$
$33$	$176001$	$168098$
$34$	$155433$	$147234$
$35$	$159608$	$152179$
$36$	$165011$	$159001$
$37$	$185001$	$179102$
$38$	$176001$	$174000$
$39$	$155433$	$153556$
$40$	$159608$	$157701$
$41$	$200000$	$1$
$42$	$110000$	$10$
$43$	$120000$	$50$
$44$	$199999$	$70$
$45$	$188888$	$100$
$46$	$200000$	$100000$
$47$	$199999$	$195000$
$48$		$100000$
$49$	$178689$	$98276$
$50$	$199998$	$88888$