题目描述

There is a circle in the plane. Both the coordinates of the center and the radius are unknown.

Chiaki found three distinct points $A$, $B$ and $C$ in the plane. And she also knows the shortest distance from each point to the circumference.

Chiaki would like to find the smallest circle according to above information.

Note that in general, a circle with infinite radius is a line. But in this problem, line is not considered as a circle.

输入格式

There are multiple test cases. The first line of input contains an integer $T$ ($1 \le T \le 2 \times 10^5$), indicating the number of test cases. For each test case:

The first line contains three integers $x_a$, $y_a$ and $d_a$ ($-100 \le x_a \le 100, y_a = 0, 1 \le d_a \le 100$) denoting the coordinates of $A$ and the shortest distance to the circumference.

The second line contains three integers $x_b$, $y_b$ and $d_b$ ($-100 \le x_b \le 100, y_b = 0, 1 \le d_b \le 100$) denoting the coordinates of $B$ and the shortest distance to the circumference.

The third line contains three integers $x_c$, $y_c$ and $d_c$ ($-100 \le x_c, y_c, d_c \le 100, d_c \ne 0$) denoting the coordinates of $C$ and the shortest distance to the circumference.

If the distance is equal to $0$, the point is on the circumference. If distance is greater than $0$, the point is inside the circle. If distance is less than $0$, the point is outside the circle and the shortest distance is the absolute value.

It is guaranteed that the minimum possible radius of the circle is at most $10^4$.

输出格式

For each test case, if there are infinite possible circles, output $-1$ in a single line. If there is no such circle, output $0$ in a single line. Otherwise, output an integer $m$ and a real number $r$ in a single line separated by one space denoting the number of possible circles and the radius of the smallest circle. You answer will be accepted if the relative error of your answer is no more than $10^{-6}$.

2
0 0 1
3 0 2
10 2 2
0 0 1
3 0 2
10 2 -2

2 10.327329213469
2 5.341730785440

提示

The image below shows the sample.

:::align{center} :::
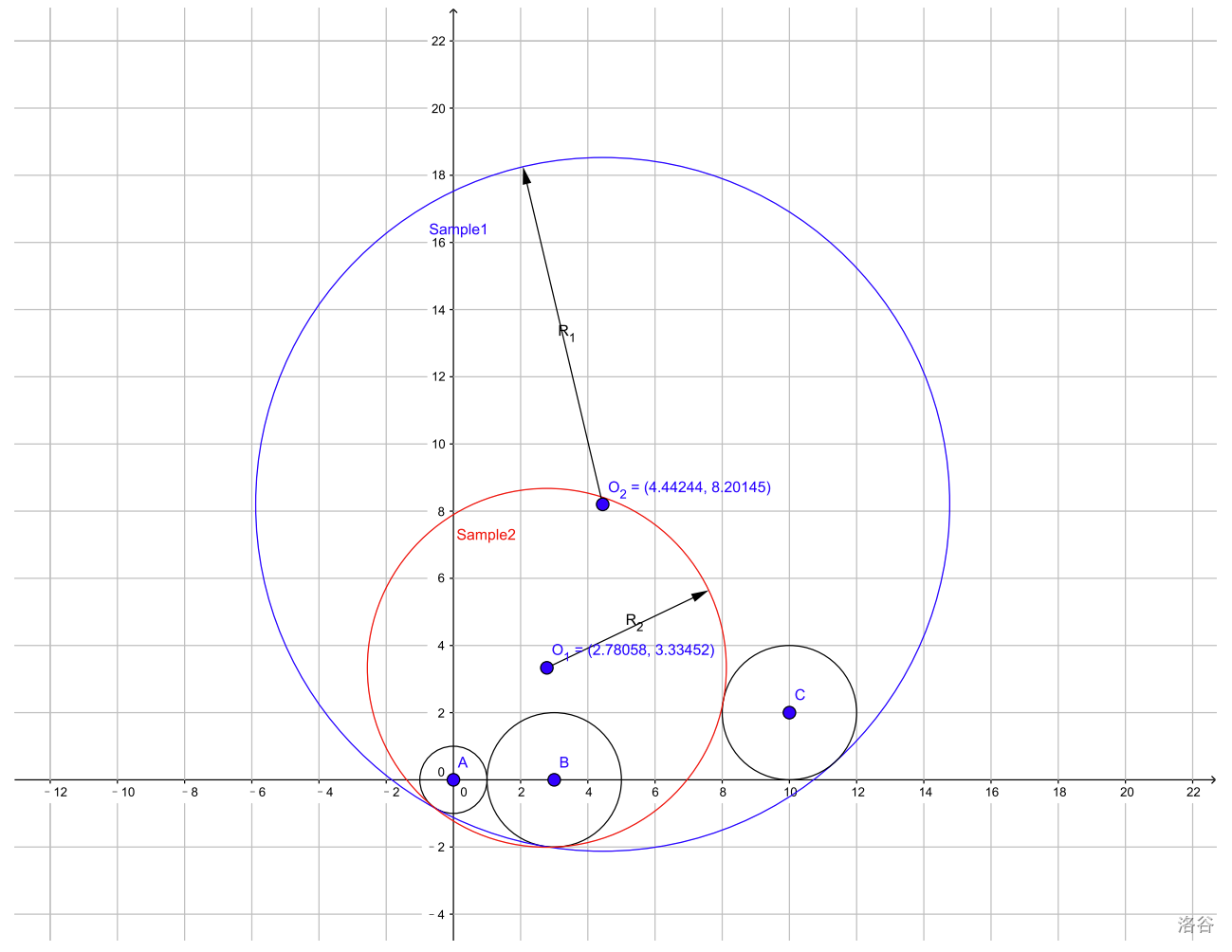