#P14108. [ZJCPC 2017] Domino Tiling
[ZJCPC 2017] Domino Tiling
题目描述
Chiaki has an rectangular chessboard. She would like to tile this board with dominoes, where a domino is a rectangle, such that:
- all the squares of the board are covered but no dominoes overlap or lie partially off the board.
- there must be no points where corners of four different dominoes meet.
The figure below shows some forbidden configurations:
:::align{center}
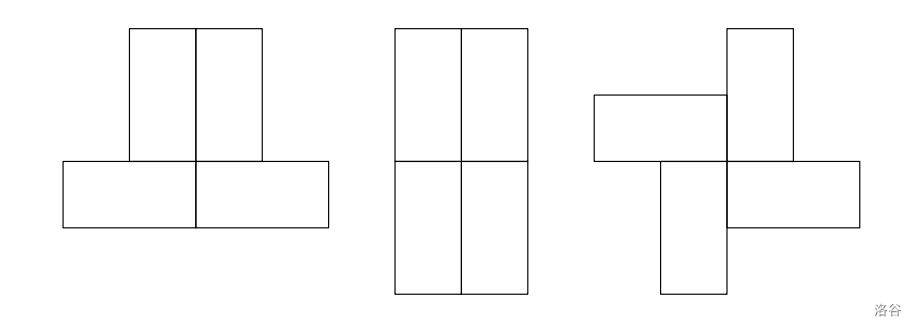 :::
:::
The figure below shows two valid tilings of chessboard:
:::align{center}
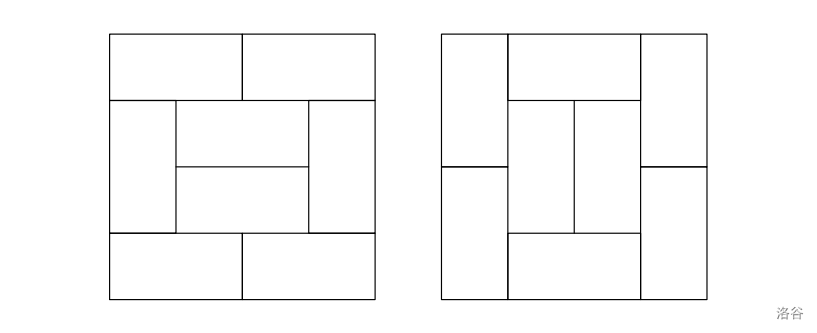 :::
:::
You also need to number the dominoes of chessboard so that no two dominoes have the same number. You can use the number from to .
输入格式
There are multiple test cases. The first line of input contains an integer , indicating the number of test cases. For each test case:
The first line contains two integers and -- the size of the rectangular chessboard.
It is guaranteed that the sum of over all test cases does not exceed .
输出格式
For each test case, output a valid chessboard described above. A valid chessboard consists of lines and each line contains integers. Each integer in the output should represent the of a domino. The grids sharing the same belong to the same domino.
If there is no solution, output "Impossible!"" (without the quotes) instead.
3
1 1
4 3
4 4
Impossible!
1 2 2
1 3 3
5 5 4
6 6 4
1 1 3 3
5 7 7 6
5 8 8 6
2 2 4 4
