题目描述

A cycle $C$ with $n$ vertices is a graph such that the vertices $i$ and $i+1$, for $i=1,\dots,n-1$, are connected by an edge and also the vertices $n$ and $1$ are connected by an edge, where the vertices of $C$ are numbered $1$ to $n$.

There are $n$ coins each of which is numbered as one of $\{1, 2,\dots, n\}$ and the numbers of two coins can be same. Initially, each vertex of $C$ has a coin among those coins. Then two vertices can swap their coins with each other. For a walk $w=v_1,v_2.\dots,v_k$) in $C$, a walk swapping is to swap two coins on $v_i$ and $v_{i+1}$ in the order of $i=1,2,\dots,k-1$. Here, a walk $w$ is a sequence of $k$($\ge 1$) vertices whose consecutive two vertices are different and adjacent in $C$, and it can be considered as the vertices visited when you traverse $C$. Also, $k$ is called the length of $w$. For a walk of length $k\ge 2$, $k-1$ swaps in its walk swapping occur, and for a walk of length one, there is no swap. The figure below shows the progress of the walk swapping for the walk $(2, 1, 4, 1)$ in the cycle with $4$ vertices.

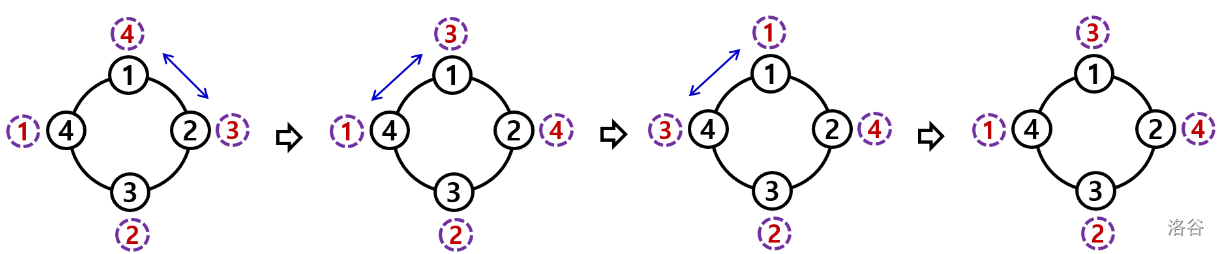
There are given the initial configuration of coins that the vertices of $C$ have in the first time and the final configuration of coins that the vertices should have in the end. You have to find a walk swapping that results in the final configuration of coins from the initial one, minimizing the total number of swaps of coins in the walk swapping.

For example, in the above figure, the number of swaps of coins in the walk swapping of the walk $(2, 1, 4, 1)$ is $3$, however, the final configuration of coins is also achieved by the walk swapping of the walk $(1, 2)$ with only one swap.

Given the number of vertices of a cycle $C$ and the initial and final configurations of coins on the vertices, write a program to output the minimum number of swaps of coins in a walk swapping resulting in the final configuration of coins from the initial one.

输入格式

Your program is to read from standard input. The input starts with a line containing one integer $n$ ($1\le n\le 3,000$), where $n$ is the number of vertices in a cycle $C$. The vertices are numbered from $1$ to $n$, and the coins on the vertices are numbered as ones of $\{1, 2, \dots , n\}$ . The second line contains $n$ integers, allowed for duplication, between $1$ and $n$, where the $i$-th integer is the coin lying on the vertex $i$ in the initial configuration of coins, for $i=1,\dots, n$. The third line contains $n$ integers, allowed for duplication, between $1$ and $n$, where the $i$-th integer is the coin lying on the vertex $i$ in the final configuration of coins, for $i=1,\dots,n$.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain the minimum number of swaps of coins in a walk swapping that results in the final configuration of coins from the initial one. If there is no such walk swapping, that is, it is impossible to result in the final configuration by any walk swapping, print -1.

4
4 3 2 1
3 4 2 1

1

6
2 1 1 2 2 1
1 2 2 2 1 1

7

6
4 1 3 6 2 5
6 2 1 3 4 5

-1