题目描述

There is a farm that borders a straight road. Suppose the road is on the $𝑥$-axis. Each boundary edge of the farm field is either horizontal or vertical. The leftmost and the rightmost edges are vertical and adjacent to the base edge which lies on the road. The length of the base edge is equal to the sum of the lengths of all other horizontal edges. See Figure C.1 (a).

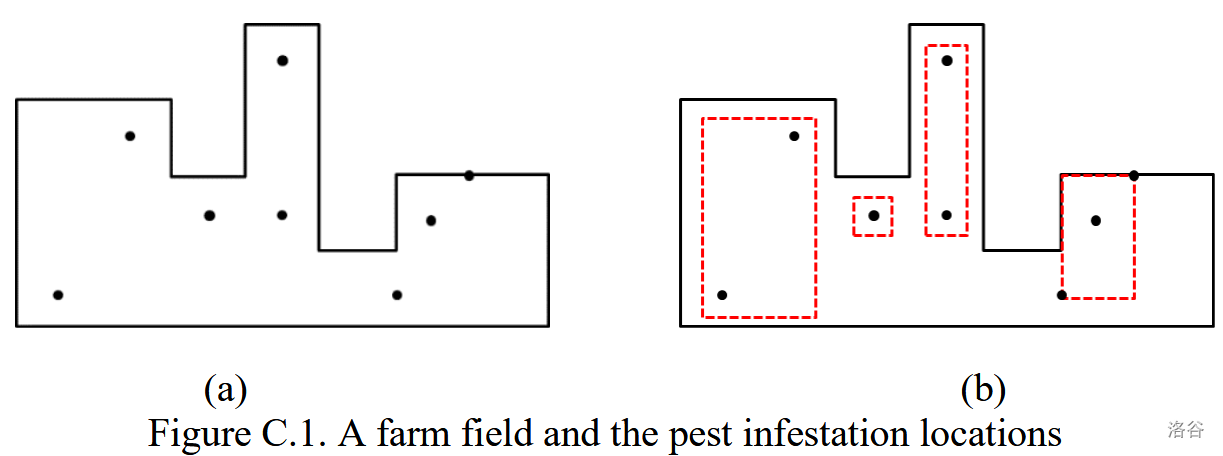
In Figure C.1, the dots on the boundary or in the interior of the farm field represent the locations where the pests have infested. To effectively eradicate the infestation, a farmer tries to divide the infested area into several rectangular areas that satisfy the following conditions.

• Each rectangular area must be contained within the farm. It is allowed for the edges of a rectangle to overlap the boundary of the farm.
• Each edge of a rectangular area is either horizontal or vertical.
• Rectangular areas are completely separated from each other, including their boundaries.
• Each pest infestation location must be contained within one of the rectangular areas. It is allowed for a pest infestation location to lie on an edge of a rectangle.

Figure C.1 (b) shows four rectangular areas covering all pest infestation locations. The farmer wants to minimize the number of rectangular areas for efficient pest management.

Given the boundary of a farm and the pest infestation locations, write a program to compute the minimum number of rectangular areas that satisfy the above conditions.

输入格式

Your program is to read from standard input. The input starts with a line containing two integers, $m$ ($4 \le m\le 100,000$) and $n$ ($0 \le n \le 100,000$), where $m$ is the number of edges of the farm field and $n$ is the number of the pest infestation locations. In the second line, $m$ integers $v_1,v_2,\dots,v_m$ ($v_1 = v_m = 0, 0 \le v_i \le 10^6$) are given, which represent the $x$-coordinates of the vertical edges and the $y$-coordinates of the horizontal edges. These vertical and horizontal edges are met alternately when traversing the upper boundary of the farm field clockwise from the left end of the base edge to the right end. From the third line, each of the $n$ lines has two integers $x$ and $y$, representing the coordinate $(x,y)$ of a pest infestation location. All locations are on the boundary or in the interior of the farm field.

输出格式

Your program is to write to standard output. Print exactly one line. The line should contain an integer representing the minimum number of rectangular areas that satisfy the above conditions.

12 8
0 30 20 20 30 40 40 10 50 20 70 0
4 5
15 26
25 15
35 15
35 35
50 5
55 15
60 20

4

4 0
0 10 50 0

0

12 3
0 3 2 6 4 1 6 4 8 2 10 0
3 5
7 3
3 1

2