题目描述

Triangle City is a city with $\frac{n(n+1)}{2}$ intersections arranged into $n$ rows and $n$ columns, where the $i$-th row contains $i$ intersections.

The intersections are connected by bidirectional roads. Formally, if we denote $(i, j)$ as the intersection on the $i$-th row and the $j$-th column, for all $1 \le j \le i < n$,

• there is a road whose length is $a_{i, j}$ connecting intersection $(i, j)$ and $(i + 1, j)$, and
• there is a road whose length is $b_{i, j}$ connecting intersection $(i, j)$ and $(i + 1, j + 1)$, and
• there is a road whose length is $c_{i, j}$ connecting intersection $(i + 1, j)$ and $(i + 1, j + 1)$.

What's more, for all $1 \le j \le i < n$, there exists a triangle whose sides are of length $a_{i, j}$, $b_{i, j}$ and $c_{i, j}$. That's why the city is called the Triangle City!

Our famous traveler BaoBao has just arrived in the Triangle City, planning to start his journey from intersection $(1, 1)$ and end his trip at intersection $(n, n)$. To fully enjoy the landscape, BaoBao would like to find the longest path from $(1, 1)$ to $(n, n)$ such that each road is passed no more than once. Please help BaoBao find such a path.

Recall that if the sides of a triangle are of length $a$, $b$ and $c$, we can infer that $a + b > c$, $a + c > b$ and $b + c > a$.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$, indicating the number of test cases. For each test case:

The first line contains an integer $n$ ($2 \le n \le 300$), indicating the size of the city.

For the following $(n - 1)$ lines, the $i$-th line contains $i$ integers $a_{i, 1}, a_{i, 2}, \dots, a_{i, i}$ ($1 \le a_{i, j} \le 10^9$), where $a_{i, j}$ indicates the length of the road connecting intersection $(i, j)$ and $(i + 1, j)$.

For the following $(n - 1)$ lines, the $i$-th line contains $i$ integers $b_{i, 1}, b_{i, 2}, \dots, b_{i, i}$ ($1 \le b_{i, j} \le 10^9$), where $b_{i, j}$ indicates the length of the road connecting intersection $(i, j)$ and $(i + 1, j + 1)$.

For the following $(n - 1)$ lines, the $i$-th line contains $i$ integers $c_{i, 1}, c_{i, 2}, \dots, c_{i, i}$ ($1 \le c_{i, j} \le 10^9$), where $c_{i, j}$ indicates the length of the road connecting intersection $(i + 1, j)$ and $(i + 1, j + 1)$.

It's guaranteed that the sum of $n$ of all test cases will not exceed $5 \times 10^3$.

输出格式

For each test case output three lines.

The first line contains one integer $l$, indicating the length of the longest path from $(1, 1)$ to $(n, n)$ such that each road is passed no more than once.

The second line contains one integer $m$, indicating the number of intersections on the longest path.

The third line contains $2m$ integers $i_1, j_1, i_2, j_2, \dots, i_m, j_m$ separated by a space, where $(i_k, j_k)$ indicates the $k$-th intersection on the longest path. Note that according to the description, there must be $(i_1, j_1) = (1, 1)$ and $(i_m, j_m) = (n, n)$.

If there are multiple valid answers, you can output any of them.

Please, DO NOT output extra spaces at the end of each line, or your solution may be considered incorrect!

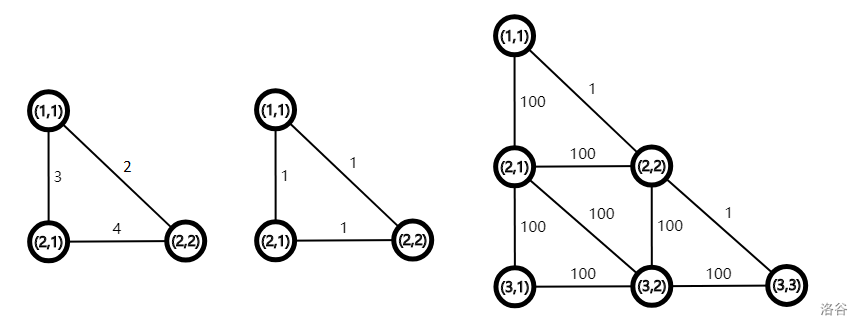
3
2
3
2
4
2
1
1
1
3
100
100 100
1
100 1
100
100 100

7
3
1 1 2 1 2 2
2
3
1 1 2 1 2 2
700
8
1 1 2 1 3 2 2 2 2 1 3 1 3 2 3 3

提示

The sample test cases are shown below:

:::align{center} :::