#P14002. [eJOI 2025] Navigation
[eJOI 2025] Navigation
题目描述
There is a connected undirected simple cactus graph with nodes and edges. Its nodes have colors (denoted with non-negative integers from to ). Initially all nodes have color . A deterministic memoryless robot explores the graph by moving from node to node. It must visit all nodes at least once and then terminate.
The robot starts at some node, which could be any of the nodes in the graph. At each step, it sees the color of its current node and the colors of all adjacent nodes in some order fixed for the current node (i.e. revisiting the node will give the robot the same sequence of adjacent nodes, even if their colors are different than before). The robot does one of the following two actions:
- Decides to terminate.
- Chooses a new (or possibly the same) color for the current node and which adjacent node to move to. The adjacent node is identified by an index from to , where is the number of adjacent nodes.
In the second case, the current node is recolored (or possibly stays the same color) and the robot moves to the chosen adjacent node. This repeats until the robot terminates or until it reaches the iteration limit. The robot wins if it visits all nodes and then terminates within the iteration limit of steps (otherwise it loses).
You should design a strategy for the robot that can solve the problem on any such cactus graph. Additionally, you should try to minimize the number of distinct colors your solution uses. Here, color always counts as used.
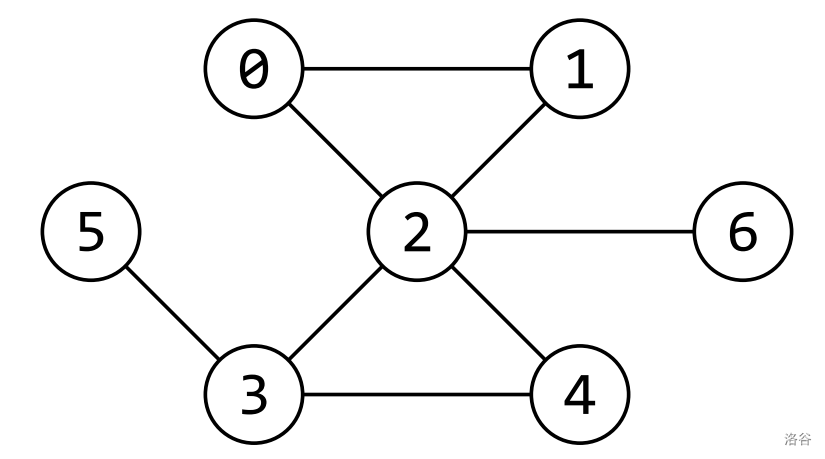
A connected undirected simple cactus graph is a connected undirected simple graph (every node is reachable from every other node; edges are bi-directional; has no self-loops or multi-edges) in which every edge belongs to at most one simple cycle (a simple cycle is a cycle that contains each node at most once). The below image is an example.
:::align{center}
 :::
:::
A robot is deterministic and memoryless, if its action depends only on its current inputs (i.e. it stores no data from step to step), and it always chooses the same action when given the same inputs.
Implementation details
The robot’s strategy should be implemented as the following function:
std::pair<int, int> navigate(int currColor, std::vector<int> adjColors)
It receives as parameters the color of the current node and the colors of all adjacent nodes (in order). It must return a pair whose first element is the new color for the current node and whose second element is the adjacency index of the node the robot should move to. If instead the robot should terminate, the function should return the pair .
This function will be called repeatedly in order to choose the actions of the robot. Since it is deterministic, if navigate was already called with some parameters, it will never be called with those same parameters again; instead its previous return value will be reused. Additionally, each test may contain subtests (distinct graphs and/or starting positions) and they may be run concurrently (i.e. your program may get alternating calls about different subtests). Finally, the calls to navigate may happen in separate executions of your program (but they may also sometimes happen in the same execution). The total number of executions of your program is . Due to all of this, your program should not try to pass information between different calls.
提示
Example
Consider the sample graph from the image in the statement, which has , and edges , , , , , , and . Additionally, since the orders of the elements in the nodes' adjacency lists are relevant, we give them in this table:
| Node | Adjacent nodes |
|---|---|
| 0 | 2, 1 |
| 1 | 2, 0 |
| 2 | 0, 3, 4, 6, 1 |
| 3 | 4, 5, 2 |
| 4 | 2, 3 |
| 5 | 3 |
| 6 | 2 |
Suppose the robot starts at node 5. Then the following is one possible (unsuccessful) sequence of interactions:
| # | Colors | Node | Call to navigate | Return value |
|---|---|---|---|---|
| 1 | 5 | navigate | ||
| 2 | 3 | navigate | ||
| 3 | 2 | navigate | ||
| 4 | 6 | navigate | ||
| 5 | 2 | navigate | ||
| 6 | 0 | navigate | ||
| 7 | 2 | navigate | ||
| 8 | 4 | navigate | ||
| 9 | 3 | navigate |
Here the robot used a total of 6 distinct colors: and (note that would have counted as used even if the robot never returned color , since all nodes start in color ). The robot ran for 9 iterations before terminating. However, it failed since it terminated without having visited node 1.
Note the call to navigate at iteration 4 would not actually happen. This is because it is equivalent to the call at iteration 1, so the grader would simply reuse the return value of your function from that call. However, this still counts as an iteration of the robot.
Note the call to navigate at iteration 4 would not actually happen. This is because it is equivalent to the call at iteration 1, so the grader would simply reuse the return value of your function from that call. However, this still counts as an iteration of the robot.
Sample grader
The sample grader does not run multiple executions of your program, so all calls to navigate will be in the same execution of your program.
The input format is the following: First (the number of subtests) is read. Then for each subtest:
- line 1: three integers - , and (the starting node of the robot);
- line (for ): two integers - and , which are the two nodes that edge connects ().
The sample grader will then print out the number of distinct colors your solution used and the number of iterations it needed before it terminated. Alternatively, it will print out an error message, if your solution failed.
By default, the sample grader prints detailed information on what the robot sees and does at each iteration. You can disable this, by changing the value of DEBUG from true to false.
Constraints
Scoring
The fraction of the points for a subtask that you get depends on - the maximum number of distinct colors your solution uses (including color 0) on any test in that subtask or any other required subtask:
- If your solution fails on any subtest, then .
- If , then .
- If , then .
- If , then .
- If , then .
Subtasks
| Subtask | Points | Required subtasks | Additional constraints | |
|---|---|---|---|---|
| 0 | - | The example. | ||
| 1 | 6 | The graph is a cycle. | ||
| 2 | 7 | The graph is a star. | ||
| 3 | 9 | The graph is a path. | ||
| 4 | 16 | The graph is a tree. | ||
| 5 | 27 | - | All nodes have at most 3 adjacent nodes and the node the robot starts at has 1 adjacent node. | |
| 6 | 28 | - | ||
| 7 | - | |||
A cycle graph has edges: for .
A star graph has edges: for .
A path graph has edges: for .
A tree is a graph with no cycles.
