题目描述

有 $n \times m$ 个点排成了 $n$ 行 $m$ 列，相邻点之间被无向带权边连接。具体来说，令 $(i, j)$ 表示位于第 $i$ 行第 $j$ 列的点，对于所有 $1 \le i, i' \le n$ 和 $1 \le j, j' \le m$，$(i, j)$ 和 $(i', j')$ 之间有边相连当且仅当 $|i - i'| + |j - j'| = 1$。

堡堡的旅行将从第一列的任意一个点 $(p, 1)$ 开始，到最后一列的任意一点 $(q, m)$ 结束。对于每条边他都可以沿着这条边的两个方向走。一条路径的距离定义为这条路径经过的边权之和。在所有从第一列到最后一列的路径中，堡堡会选择最短的路径。

小青鱼希望堡堡享受这段旅行，于是他尝试在堡堡出发前增加一些边的权值。具体来说，小青鱼每次操作可以选择一条边，将它的权值增加 $1$。小青鱼希望在他修改后，堡堡旅行的距离恰好增加了 $k$。请帮助他求出最少需要进行多少次操作，并输出方案。

输入格式

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数，对于每组测试数据：

第一行输入三个整数 $n$，$m$ 和 $k$（$1\leq n\times m\leq 500$，$2\leq n,m\leq 500$，$1\leq k\leq 100$）表示行数，列数和最短路径距离的增加量。

对于接下来的 $n$ 行，第 $i$ 行输入 $(m - 1)$ 个整数 $r_{i,1}, r_{i,2}, \cdots, r_{i,m-1}$（$1\leq r_{i,j}\leq 10^9$），其中 $r_{i,j}$ 表示连接 $(i,j)$ 和 $(i,j+1)$ 的边权。

对于接下来的 $(n - 1)$行，第 $i$ 行输入 $m$ 个整数 $c_{i,1}, c_{i, 2}, \cdots, c_{i,m}$（$1\leq c_{i,j}\leq 10^9$），其中 $c_{i,j}$ 表示连接 $(i,j)$ 和 $(i+1,j)$ 的边权。

保证所有数据 $n\times m$ 之和不超过 $5 \times 10^3$。

输出格式

对于每组数据：

首先输出一行一个整数表示最少需要的操作次数。

接下来输出 $n$ 行，第 $i$ 行输出 $(m - 1)$ 个由单个空格分隔的整数 $r'_{i,1}, r'_{i,2}, \cdots, r'_{i,m-1}$（$1\leq r'_{i,j}\leq 2\times 10^9$），其中 $r'_{i,j}$ 表示完成所有操作后连接 $(i,j)$ 和 $(i,j+1)$ 的边权。

接下来输出 $(n - 1)$ 行，第 $i$ 行输出 $m$ 个由单个空格分隔的整数 $c'_{i,1}, c'_{i,2}, \cdots, c'_{i,m}$（$1\leq c'_{i,j}\leq 2\times 10^9$），其中 $c'_{i,j}$ 表示完成所有操作后连接 $(i,j)$ 和 $(i+1,j)$ 的边权。

如果有多种合法答案，输出任意一种。

请不要在行末输出多余空格，否则您的答案可能会被认为是错误的！

2
3 4 6
2 1 15
7 1 9
13 3 2
3 6 1 2
5 2 15 3
3 3 3
1 1
2 2
3 3
1 1 1
2 2 2

9
2 3 15
7 1 10
13 3 4
3 6 3 2
5 4 15 3
4
4 1
3 2
3 3
1 1 1
2 2 2

提示

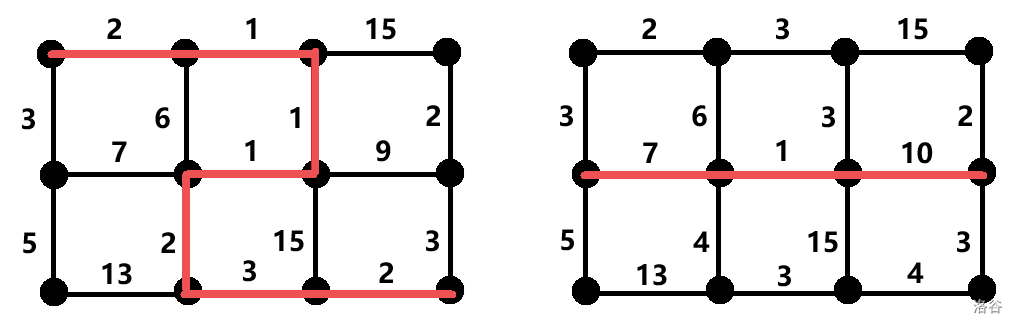
第一组样例数据如下图所示。左边的是原图，右边的是增加一些边的权值之后的图。每张图的最短路用红色线条表示。

:::align{center} :::