题目描述

有一棵 $n$ 个节点的有根树，节点编号从 $1$ 到 $n$，其中节点 $1$ 为根。每个节点都有一个颜色， 要么是红色，要么是黑色。

称一个节点是好的，若每一条以该节点为起点，以该节点任意一个后代叶子节点为终点的简单路径中，都包含相同数量的黑色节点。称一棵树是完美的，若树中每个节点都是好的。

令 $R_k$ 表示以节点 $k$ 为根的子树。对于每个 $1 \le k \le n$，回答以下询问：如果您可以任意选择一些节点并改变它们的颜色（也就是说，把红色节点改成黑色，以及把黑色节点改成红色），至少需要选择几个节点才能让 $R_k$ 变得完美。

请回忆：简单路径不会多次经过同一条边。

同时请回忆：以节点 $k$ 为根的子树是一棵由节点 $k$ 所有后代组成的有根树，并以节点 $k$ 为根。请注意，每个节点都是它自己的后代。

输入格式

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数，对于每组测试数据：

第一行输入一个整数 $n$（$2 \le n \le 10^5$）表示树中节点的数量。

第二行输入一个长度为 $n$ 的字符串 $s_1s_2\cdots s_n$（$s_i \in \{0, 1\}$）。若 $s_i = 0$ 则节点 $i$ 是红色节点；若 $s_i = 1$ 则节点 $i$ 是黑色节点。

第三行输入 $(n - 1)$ 个整数 $p_2, p_3, \cdots, p_n$（$1 \le p_i < i$），其中 $p_i$ 是节点 $i$ 的父节点。

保证所有数据 $n$ 之和不超过 $10^6$。

输出格式

每组数据输出一行 $n$ 个由单个空格分隔的整数，其中第 $i$ 个整数表示至少需要选择几个节点才能让 $R_i$ 变得完美。

请不要在行末输出多余空格，否则您的答案可能会被认为是错误的！

2
9
101011110
1 1 3 3 3 6 2 2
4
1011
1 1 3

4 1 2 0 0 0 0 0 0
2 0 0 0

提示

:::align{center} :::

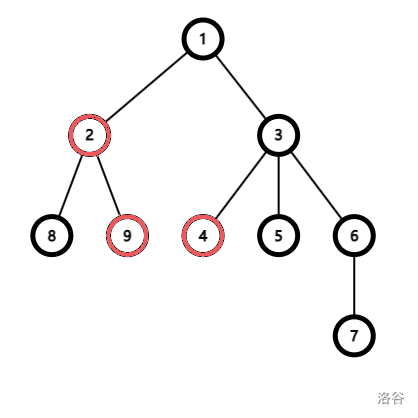
我们展示第一组样例数据。

为了让 $R_1$ 变得完美，我们可以改变节点 $2$，$4$，$6$ 和 $9$ 的颜色。改变之后，所有从节点 $1$ 到后代叶子节点的路径均包含 $3$ 个黑色节点，所有从节点 $2$ 到后代叶子节点的路径均包含 $2$ 个黑色节点，所有从节点 $3$ 到后代叶子节点的路径均包含 $2$ 个黑色节点。由于节点 $4$ 到 $9$ 都只有一个后代叶子节点，所以它们一直都是好的。

为了让 $R_2$ 变得完美，我们可以改变节点 $8$ 的颜色。改变之后，所有从节点 $2$ 到后代叶子节点的路径均包含 $0$ 个黑色节点。由于节点 $8$ 和 $9$ 都只有一个后代叶子节点，所以它们一直都是好的。