题目描述

继 2018，2019，2020，2021 和 2022 年成功承办赛事之后，南京航空航天大学（NUAA）将连续第六年承办国际大学生程序设计竞赛（ICPC）。

在 2018 与 2019 年，“中二之力”队与“三个顶俩”队为清华大学赢得了冠军。在 2020，2021 与 2022 年，北京大学的“逆十字”队赢得三连冠。今年，将会有约 $330$ 支队伍参与南京站的竞赛。本次竞赛将会颁发至多 $33$ 项金奖，$66$ 项银奖与 $99$ 项铜奖（数字仅供参考）。让我们期待选手们出色的表现！

更棒的是，因为疫情已经结束，我们终于可以相聚南京参与这场精彩的比赛。我们想要感谢竞赛组委会与志愿者们的努力付出。感谢你们为本次竞赛做出的贡献！

:::align{center} 2018 国际大学生程序设计竞赛亚洲区域赛（南京站） :::

在 2018 年的竞赛中，K 题《袋鼠谜题》要求选手为以下游戏构造一个操作序列：

谜题由一个 $n$ 行 $m$ 列的网格（$1 \le n, m \le 20$）组成，且有一些（至少 $2$ 只）袋鼠位于网格中。玩家的目标是控制袋鼠并把它们聚集在同一个格子中。一些格子里有墙，袋鼠无法进入这些有墙的格子，而其它格子是空的。袋鼠可以从一个空格子移动到上，下，左，右相邻的另一个空格子中。
游戏开始时，每个空格子里都有一只袋鼠。玩家可以通过键盘上 U，D，L，R 四个按键控制袋鼠的移动。所有袋鼠会同时根据您按下的按键移动。
选手需要构造一个长度至多为 $5 \times 10^4$ 且由 U，D，L，R 组成的操作序列以达成目标。

在 2020 年的竞赛中，A 题《啊，昨日重现》要求选手构造一张输入地图，以证明以下代码并不是上述问题的解：

#include <bits/stdc++.h>
using namespace std;
string s = "UDLR";
int main()
{
  srand(time(NULL));
  for (int i = 1; i <= 50000; i++) putchar(s[rand() % 4]);
  return 0;
}

在 2021 年的竞赛中，A 题《呀，昨日再次重现》同样要求选手为以下游戏构造操作序列：

本题中，网格中的每个格子都有恰好一只袋鼠。您需要构造一个仅由字符 U，D，L 和 R 组成的操作序列。在应用该操作序列后，所有袋鼠必须聚集在指定格子 $(a,b)$ 中。操作序列的长度不能超过 $3(n-1)$。同往常一样，所有袋鼠会根据您的命令同时移动。

在 2022 年的竞赛中，A 题《停停，昨日请不要再重现》要求选手解决以下计数问题：

本题中，网格中的每个格子（除了一个格子是洞）都恰好有一只袋鼠。给定操作序列，所有走出网格外或踩到洞上的袋鼠都会被移除。给定所有操作后剩余的袋鼠数量，求有几个位置可能是洞。

在 2023 年的竞赛中，袋鼠题又回来啦！我们不知道为什么命题组的成员们那么喜欢袋鼠，但题目如下：

给定一张 $n$ 行 $m$ 列的网格，每个格子要么是洞，要么是空地。每个空地都恰好有一只袋鼠。

相似地，袋鼠可以被键盘上的 U，D，L，R 键控制。所有袋鼠会同时根据按下的按键移动。具体来说，对于一只位于第 $i$ 行第 $j$ 列的格子（用 $(i,j)$ 表示）上的袋鼠：

• 按键 U：它会移动到 $(i-1,j)$。
• 按键 D：它会移动到 $(i+1,j)$。
• 按键 L：它会移动到 $(i,j-1)$。
• 按键 R：它会移动到 $(i,j+1)$。

如果一只袋鼠踩到了洞或者移动到了网格外面，它将被从网格上移除。如果完成一系列操作后（操作序列可以为空）恰有一只袋鼠留在网格上，那么这只袋鼠就是赢家。

您需要解决的问题是：对于每只袋鼠，判断是否存在一个操作序列使得它成为赢家。输出可能成为赢家的袋鼠总数。

输入格式

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数，对于每组测试数据：

第一行输入两个整数 $n$ 与 $m$（$1 \le n, m \le 10^3$，$1 \le n \times m \le 10^3$）表示网格的行数和列数。

对于接下来 $n$ 行，第 $i$ 行输入一个长度为 $m$ 的字符串 $s_{i, 1}s_{i, 2} \cdots s_{i, m}$，每个字符要么是 $\texttt{.}$（点号，ascii: 46）要么是 $\texttt{O}$（大写字母，ascii: 79）。如果 $s_{i, j}$ 是 $\texttt{.}$ 则格子 $(i, j)$ 是空地；如果 $s_{i, j}$ 是 $\texttt{O}$ 则格子 $(i, j)$ 是洞。

保证所有数据 $n \times m$ 之和不超过 $5 \times 10^3$。

输出格式

每组数据输出一行一个整数，表示共有几只袋鼠满足存在一个操作序列使得它成为赢家。

4
2 5
.OO..
O..O.
1 3
O.O
1 3
.O.
2 3
OOO
OOO

3
1
0
0

提示

样例数据解释如下。我们用 W 表示接下来成为赢家的袋鼠，用 K 表示其它袋鼠。

对于第一组样例数据，初始位于 $(1, 4)$，$(1, 5)$ 和 $(2, 5)$ 的袋鼠可能成为赢家。以下展示可能的操作序列：

:::align{center} :::

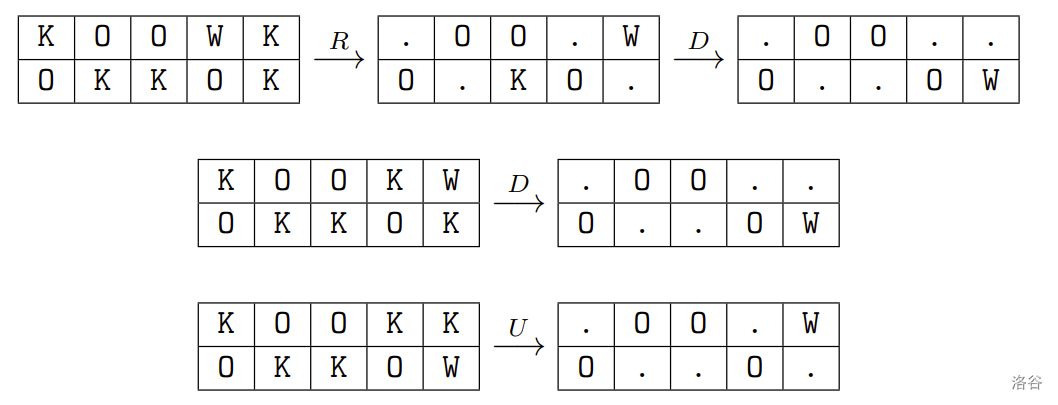对于第二组样例数据，因为只有一只袋鼠，无需任何操作即可让它成为赢家。

对于第三组样例数据，因为任何操作都会让两只袋鼠同时被移除，所以没有任何可能的赢家。

对于第四组样例数据，因为没有袋鼠，所以没有任何可能的赢家。