题目描述

在听说了哥德堡下水道里有变异巨鼠的传闻后，你最亲密的朋友们决定逃往美妙的斯德哥尔摩。 在逃亡途中，你的朋友们注意到，通往斯德哥尔摩的路上奇怪地有很多路牌，指向隆德附近的各个小村庄。此外，路牌上的数字似乎很可疑，因为一些路牌上的信息与其他路牌相矛盾。

在你的朋友们经过的 $N$ 个路牌上，每个路牌都标有到隆德所有 $M$ 个村庄的距离。 这些距离被取整为整数，因为实际距离不一定是整数。 由于你的好朋友们碰巧拥有过目不忘的记忆力，他们清楚地记得路牌上标明的具体距离。 然而，你的朋友们不记得他们是在何时或以何种顺序看到这 $N$ 个路牌的。

你可以假设斯德哥尔摩、哥德堡和隆德的小村庄都位于一条直线上。 此外，你可以假设所有的城市、村庄和路牌都非常小，可以表示为这条直线上的点。 你还可以假设，隆德的村庄都不会位于两个路牌之间。 换句话说，隆德的村庄和路牌位于哥德堡的两侧。

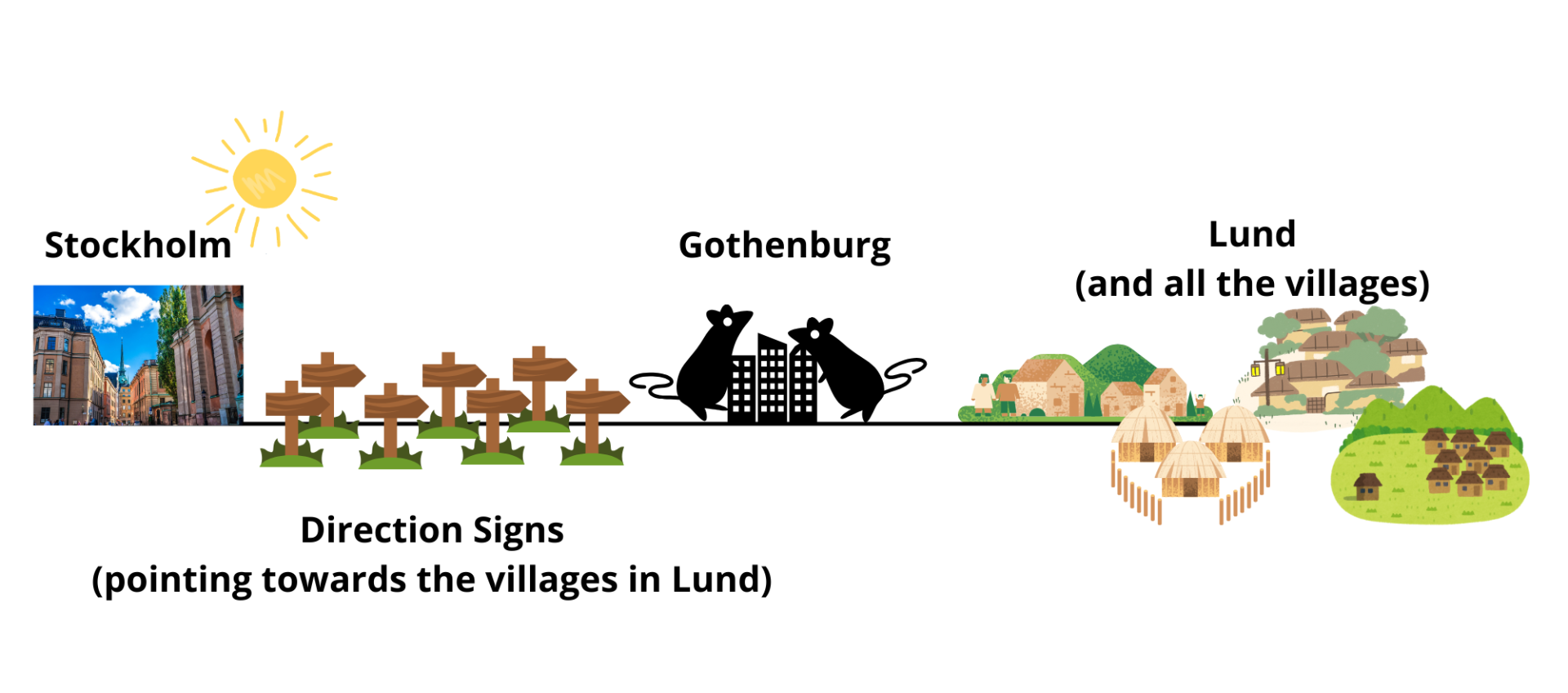
上图说明了隆德的村庄和路牌如何位于哥德堡的不同侧。

给定你的朋友们看到的这 $N$ 个路牌，请问最多能选出多少个路牌，使得它们上面给出的距离信息互不矛盾？ 最后，你还可以假设，至少有 $20\%$ 的路牌是完全正确的，并且它们之间不会产生任何矛盾。

输入格式

第一行包含两个整数 $N$ 和 $M$（$1 \leq N \leq 1000$, $1 \leq M \leq 200$），分别代表你的朋友们看到的路牌数量和隆德的村庄数量。

接下来的 $N$ 行输入，每行包含 $M$ 个整数。第 $i$ 行包含整数 $d_{i,1}, d_{i,2}, \ldots, d_{i,M}$（$1 \leq d_{i,j} \leq 10^6$），描述了第 $i$ 个路牌上写的 $M$ 个距离。 也就是说，在第 $i$ 个路牌上，它标明了从路牌 $i$ 到村庄 $j$ 的距离向下取整后是 $d_{i,j}$，对于所有 $1 \leq j \leq M$ 均成立。

输出格式

首先，在单行上输出一个整数 $t$，表示最多能选出的互不矛盾的路牌数量。

在第二行，输出 $t$ 个整数，代表这些路牌的索引。输出的索引顺序必须满足：第一个索引对应的路牌离哥德堡和所有隆德村庄最远，最后一个索引对应的路牌离哥德堡和所有隆德村庄最近。

由于人们在处理 0-indexed 的事物时会感到困惑，我们希望路牌是 1-indexed 的。因此，输入中的第一个路牌索引为 1，最后一个路牌索引为 $N$。

如果存在多个有效的解决方案，你的程序可以输出其中任意一个。

3 2
2 2
2 3
3 2

2
2 1

5 1
17
12
2
8
20

5
5 1 2 4 3

5 2
1 10
3 10
5 10
7 10
9 10

1
1

提示

样例解释

样例 1 解释

想象一条 $x$ 轴数轴。 第二个路牌可以放在位置 $x = 1$ 处，第一个路牌在 $x = 1.5$ 处，第一个村庄在 $x = 3.5$ 处，第二个村庄在 $x = 4$ 处。

同样，也可以为 1 号和 3 号路牌找到一种符合题意的构造。

很明显，1 号和 2 号路牌是相互矛盾的，这意味着不存在一种构造能同时使用所有 3 个路牌。

样例 2 注释

请注意，尽管所有路牌都指向同一个村庄，但它们将距离向下取整到了不同的数值。

样例 3 注释

请注意，任意一对路牌都会导致矛盾；在这种情况下，任何单个路牌都是一个正确的答案。

子任务

本题采用捆绑测试。 | 子任务编号 | 得分 | 限制 | |:-:|:-:|---| | $1$ | $21$ | $N \leq 15, M \leq 50$ | | $2$ | $31$ | $N \leq 100, M \leq 50$ | | $3$ | $18$ | $N \leq 500, M \leq 50$ | | $4$ | $30$ | 无额外约束 |