题目描述

你正在前往瑞典信息学奥林匹克竞赛的决赛，该决赛在查尔姆斯理工大学举行。然而，你却在大学的地下室迷路了。你的方向感不佳，更糟糕的是地下室的设计非常奇怪。

图 1：查尔姆斯的黑暗密室

地下室共有 $2 \le N \le 1000$ 层。在地面层，只有一个大房间。对于所有其他房间，其正上方都存在一个房间。每向下一层，房间的大小都会减半。在每个房间 $i$ 的下方，最多有两个房间 $l_i$ 和 $r_i$，每个房间的大小都恰好是房间 $i$ 的一半。$l_i$ 和 $r_i$ 可能只存在一个，或者两者都存在，或者两者都不存在。如果两个房间直接相邻，你可以通过门在它们之间移动；如果一个房间在另一个房间的正上方，你可以通过楼梯移动。你目前在地下室的某个房间里，并且你知道决赛也在地下室的某个地方举行。

路径是指一系列通往相邻房间的步骤。对于从你当前所在房间到决赛所在房间的某条路径 $v$，令 $A_v$ 为你穿过门的次数，令 $B_v$ 为你上下楼梯的次数。路径的长度定义为 $L_v = A_v + B_v$。你现在想去参加决赛。为了帮助你，你下载了“校园地图”应用。“校园地图”应用的程序设计目标是找到前往目的地的路径长度，其中需要上下楼梯的次数最少。在所有通往决赛所在房间的可能路径 $v$ 中，应用会找出所有使 $B_v$ 值最小的路径。在这些路径中，它会选择使 $L_v$ 值最小的那一条。然后，它会给出这条路径的长度 $L_v$ 值。

由于应用运行缓慢，你最多只能查询它 500 次。你也没有时间移动到其他房间超过 5000 次。

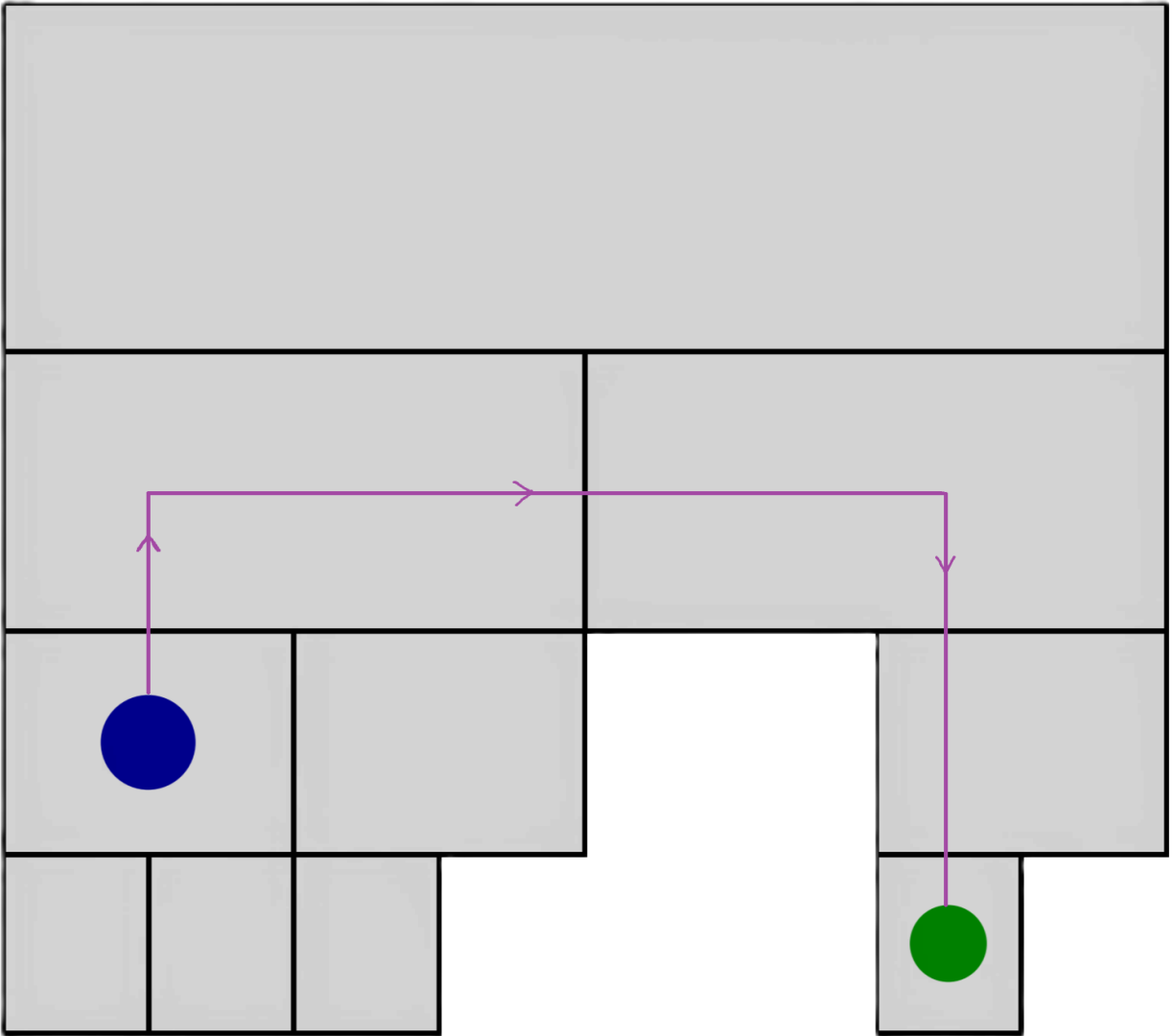
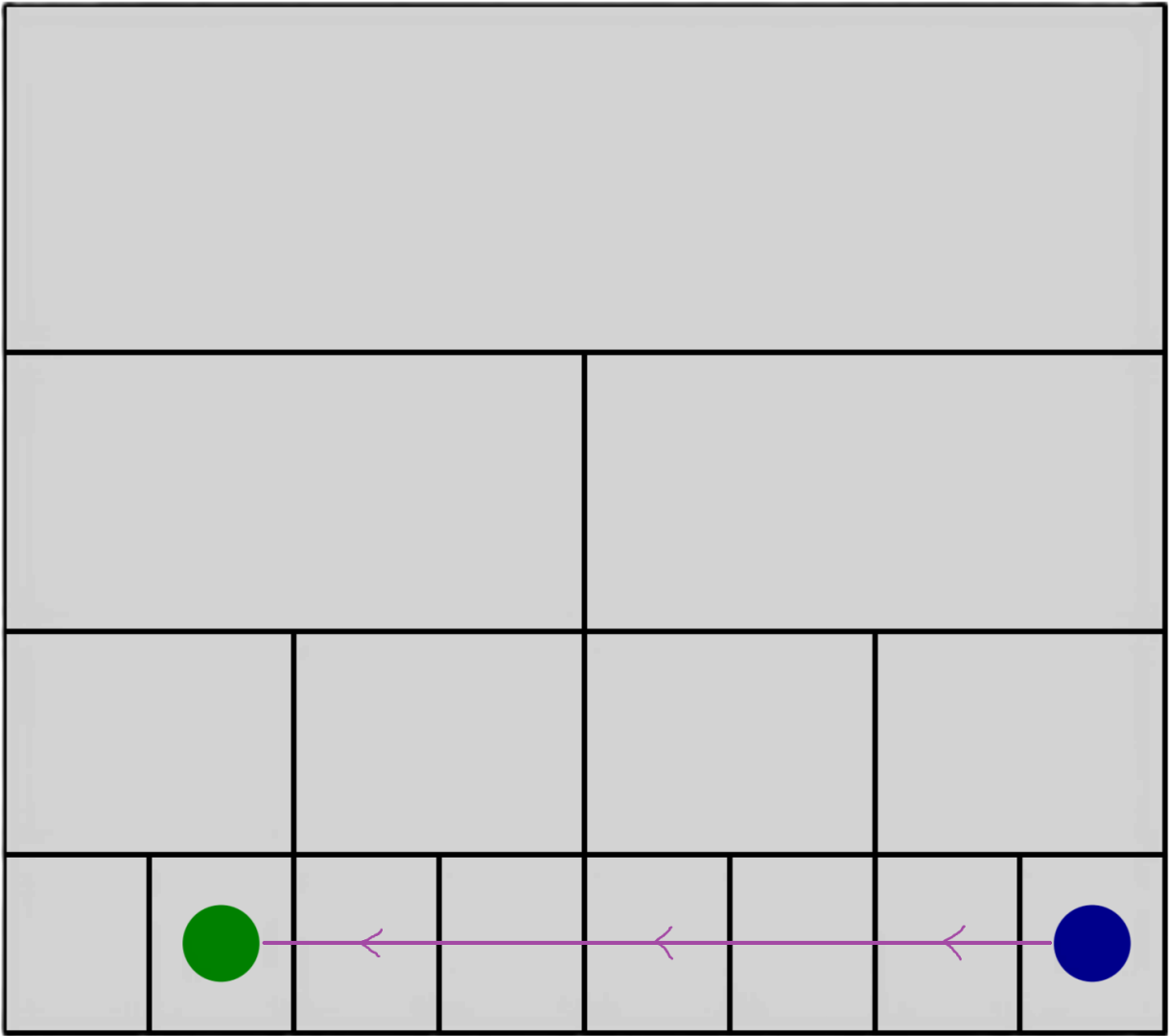
图 2：示例情况 1 和 2 中的地下室。蓝色圆圈是你的起始位置，绿色圆圈显示决赛所在的房间。在两张图中，“校园地图”应用找到的路径都用紫色表示。在示例情况 1 中，这条路径经过三个楼梯和一个门。在示例情况 2 中，这条路径经过零个楼梯和六个门。

交互格式

首先，你会获得当前所在房间的信息。这会以一个长度为五的二进制字符串给出，其中每个字符为“1”表示你可以朝某个方向移动，否则为“0”。字符的顺序依次表示你是否可以向上、向右、向右下、向左下、向左移动。因此，字符串 01001 意味着你可以向右和向左移动，但不能向其他方向移动。

然后，你可以选择移动到相邻房间，或者使用“校园地图”应用。要移动到相邻房间，你需要写入“up”、“right”、“downright”、“downleft”或“left”中的任意一个字符串。然后，你会获得新房间的信息，格式与上述相同。

要使用该应用，你需要写入“app”。该应用会计算从你当前位置到目标的最短路径长度，该路径使用的楼梯数量尽可能少。由于该应用对整数溢出非常敏感，如果路径长度超过 $10^9$，它将崩溃。在这种情况下，应用会写入 -1。否则，会写入到目标的路径长度。

当你到达目的地时，你应该打印“here”，然后你的程序应该终止。

请确保在每次查询后刷新输出，否则你可能会遇到“时间限制超出”。在 C++ 中可以使用 cout << flush; 或 fflush(stdout); 完成；在 Python 中使用 stdout.flush()；在 Java 中使用 System.out.flush()。

输入格式

见「交互格式」。

输出格式

见「交互格式」。

11110

4

11110

10101

2

10010

10000

0

app

up

right

app

downright

downleft

app

here

10001

6

10111

4

11111

11111

11110

11001

app

up

app

left

left

left

downright

here

提示

子任务

本题采用捆绑测试。 | 子任务编号 | 得分 | 限制 | |:-:|:-:|---| | $1$ | $5$| $N = 2$ | | $2$ | $10$ | $N \le 10$ | $3$ | $10$ | $N \le 250$ | | $4$ | $16$ | 不在最底层的所有房间下方都有两个房间。 | | $5$ | $13$ | $N \le 500$ | | $6$ | $21$ | $N \le 950$ | | $7$ | $25$ | $N \le 1000$ |