题目描述

A young biologist is studying evolutionary history and has come across phylogenetic trees. A phylogenetic tree shows evolutionary relationships among various biological species. It is presented in a planar embedding with its leaves arranged in a circular manner for a better visual presentation. We are dealing with an unrooted tree, where the leaves are nodes of degree 1. All nodes of the tree are colored, which makes distinguishing different species easier.

Our biologist is using graph visualization software which needs some help to produce a desired layout. Therefore, she has decided to add edges between adjacent leaves in the planar embedding. The tree has at least 3 leaves, which she connects in a cycle. The illustration below shows an example of such (uncolored) tree with additional edges between adjacent leaves indicated by dashed lines.

:::align{center} 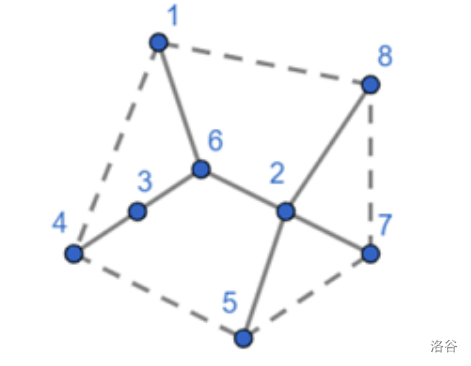:::align

Now that the visualization is done, she is interested in the number of ways to color the nodes of this graph with $K$ colors. Every pair of adjacent nodes should have a different color for easier visual recognition. Write a program that will read the description of her graph structure and compute the number of colorings.

输入格式

The first line contains integers $N$, $M$ and $K$. The edges of the graph are given in the following $M$ lines as pairs of endpoints $A_i$ and $B_i$ (the nodes of the graph are numbered from 1 to $N$). All integers in the same line are separated by a space.

It is guaranteed that the graph was obtained from a planar embedding of a tree (acyclic connected undirected graph) by also connecting its leaves in a circular manner. The graph will not contain loops or parallel edges (i.e. multiple edges between the same pair of nodes).

输出格式

Output the number of colorings modulo $1\ 000\ 000\ 007$.

8 12 3
2 5
3 6
2 6
5 4
4 1
1 6
7 5
2 7
3 4
2 8
7 8
1 8

24

提示

Input limits

• $4 \leq N \leq 10^5$
• $1 \leq K \leq 10^5$