题目描述

Yuki 有一棵仅包含根结点 $1$ 的有根树 $T$ 和一个变量 $n$，初始时 $n=1$。

给定 $q$ 次操作。操作有以下 $2$ 种：

• $1\ u_i\ x_i$：在 $u_i$ 的第 $x_i$ 个儿子后插入结点 $n+1$；特殊地，若 $x_i=0$，则表示将结点 $n+1$ 作为 $u_i$ 的第 $1$ 个儿子插入。$u_i$ 的其余儿子的相对顺序不变。设 $u_i$ 的儿子个数为 $s_{u_i}$，则保证 $1 \le u_i \le n$ 且 $0 \le x_i \le s_{u_i}$。在执行此操作后 $n$ 的值变为 $n+1$。

• $2\ v_i\ k_i$：查询对树 $T$ 进行 $k_i$ 次左儿子右兄弟变换后结点 $v_i$ 的父亲结点。其中，左儿子右兄弟变换指：对于树 $T$ 上的结点 $u$，将结点 $u$ 在原树中的第一个儿子作为结点 $u$ 在新树上的左儿子，将结点 $u$ 在原树中的下一个兄弟作为结点 $u$ 在新树上的右儿子。保证 $2 \le v_i \le n$ 且 $1 \le k_i \le 10^9$。注意，此操作不会真的对树 $\boldsymbol T$ 进行 $\boldsymbol{k_i}$ 次左儿子右兄弟变换，也就是说在执行此操作后树形态不变。

你需要对于每个 $2$ 操作求出答案。

输入格式

本题有多组测试数据。

输入的第一行包含两个正整数 $c,T$，分别表示测试点编号和测试数据组数。样例满足 $c=0$。

接下来依次输入每组测试数据。对于每组测试数据：

• 第一行一个正整数 $q$。
• 接下来 $q$ 行，第 $i$ 行三个整数 $o_i,u_i,x_i$ 或 $o_i,v_i,k_i$，格式同题目描述。

输出格式

对于每组测试数据中的每个 $2$ 操作，输出一行一个整数表示答案。

0 2
8
1 1 0
1 2 0
2 3 1
1 3 0
1 1 0
1 4 0
1 4 1
2 7 1
8
1 1 0
2 2 2
2 2 2
1 2 0
2 3 1
1 3 0
1 4 0
2 4 3

2
6
1
1
2
3

提示

样例 1 解释

该样例包含两组测试数据，对于第一组测试数据：

• 第 $1$ 次操作插入结点 $2$ 作为结点 $1$ 的儿子结点。

• 第 $2$ 次操作插入结点 $3$ 作为结点 $2$ 的儿子结点。

• 此时树包含 $2$ 条边 $(1, 2), (2, 3)$，经过 $1$ 次左儿子右兄弟变换后，树仍为 $(1, 2), (2, 3)$，$3$ 的父亲结点为 $2$。

• 接下来进行 $4$ 次结点插入操作，操作结束后的树形如：

  

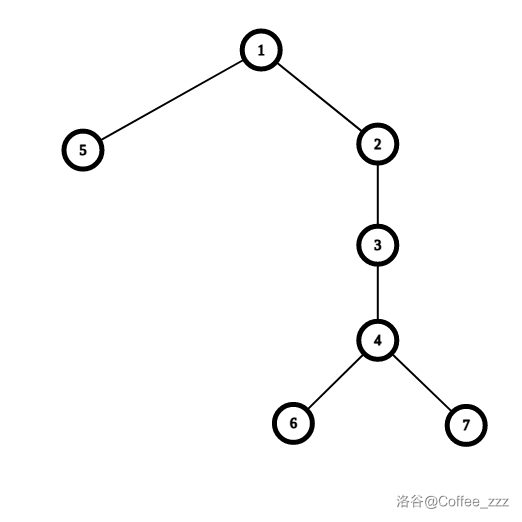
• 经过 $1$ 次左儿子有兄弟变换后，树形如：

  

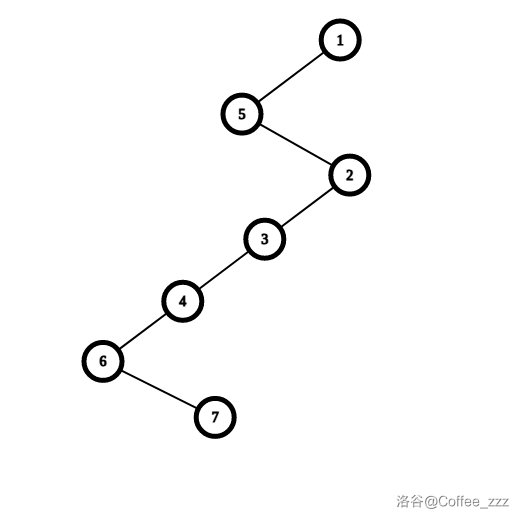
  此时结点 $7$ 的父亲结点为 $6$。

数据范围

对于所有测试数据，保证：

• $1 \le T \le 3$；
• $1 \le q \le 10^6$；
• $o_i \in \{1,2\}$，$1 \le u_i \le n$，$0 \le x_i \le s_{u_i}$，$2 \le v_i \le n$，$1 \le k_i \le 10^9$。

测试点编号	$q \le$	$k_i$	特殊性质
$1\sim3$	$10^2$	$\le10^2$	无
$4,5$	$3 \times 10^3$	$=1$
$6,7$		$=10^9$
$8\sim10$		$\le10^9$
$11,12$	$5 \times 10^5$	$=1$
$13,14$		$=10^9$
$15$		$\le10^9$	A
$16,17$			B
$18,19$			C
$20\sim22$			无
$23\sim25$	$10^6$

• 特殊性质 A：对于所有 $1$ 操作，均有 $u_i=1$。
• 特殊性质 B：对于所有满足 $1\le i \lt j \le q$ 的正整数 $i,j$，均有 $op_i \le op_j$。
• 特殊性质 C：对于所有 $1$ 操作，均有 $x_i=cnt_{u_i}$。