题目背景

This is an interactive problem

题目描述

You are given a tree of $n$ vertices. The tree is a graph such that there is exactly one simple path between every pair of vertices. It's also guaranteed that at least one vertex is directly connected by an edge to at least 3 vertices. One of the vertices is the root, and your task is to find it. In order to do this, you are allowed to ask queries of the following form:

• For a given set $a_1, a_2, \ldots, a_m$ of vertices, check if their lowest common ancestor is in this set.

A vertex $v$ is a common ancestor of a set $S$ of vertices if the paths from all vertices in $S$ to the root pass through $v$. The lowest common ancestor (LCA) of a set $S$ of vertices is the common ancestor of $S$ which is farthest from the root.

Interaction

Start the interaction by reading a single integer $n$ ($4 \leq n \leq 500$) - the number of vertices.

Then read next $n - 1$ lines. The $i$-th line will contain two integers $a_i, b_i$ ($1 \leq a_i, b_i \leq n$), indicating that there is an edge between vertices $a_i, b_i$ in the tree.

It's guaranteed that these $n - 1$ edges form a tree and at least one vertex is directly connected by an edge to at least 3 vertices.

To ask a query, firstly output "?", then the integer $m$, and then $m$ distinct integers $a_1, a_2, \ldots, a_m$ ($1 \leq m \leq n, 1 \leq a_i \leq n$, all $a_i$ are distinct) - vertices, for which you want to check if their LCA is among them.

As a response, the interactor will output "YES" if their LCA is one of $a_1, a_2, \ldots, a_m$, and "NO" otherwise.

You can ask at most 1000 queries, but you'll get a different number of points depending on how many queries you ask. Outputting the answer does not count as a query. Please, look at the scoring section for the details.

When you have identified the root, output the symbol "!" and then one integer $v$ ($1 \leq v \leq n$) - the root. Then terminate your program.

After printing a query do not forget to output end of line and flush the output. To do this, use:

• fflush(stdout) or cout.flush() in C++;
• stdout.flush() in Python;

It is guaranteed that for each test case, the tree and its root are fixed before the start of the interaction. In other words, the interactor is not adaptive.

7
4 1
1 2
4 3
3 5
3 6
4 7

NO

YES

NO

YES

? 2 5 6

? 3 6 3 5

? 2 1 7

? 2 4 6

! 4

提示

Note

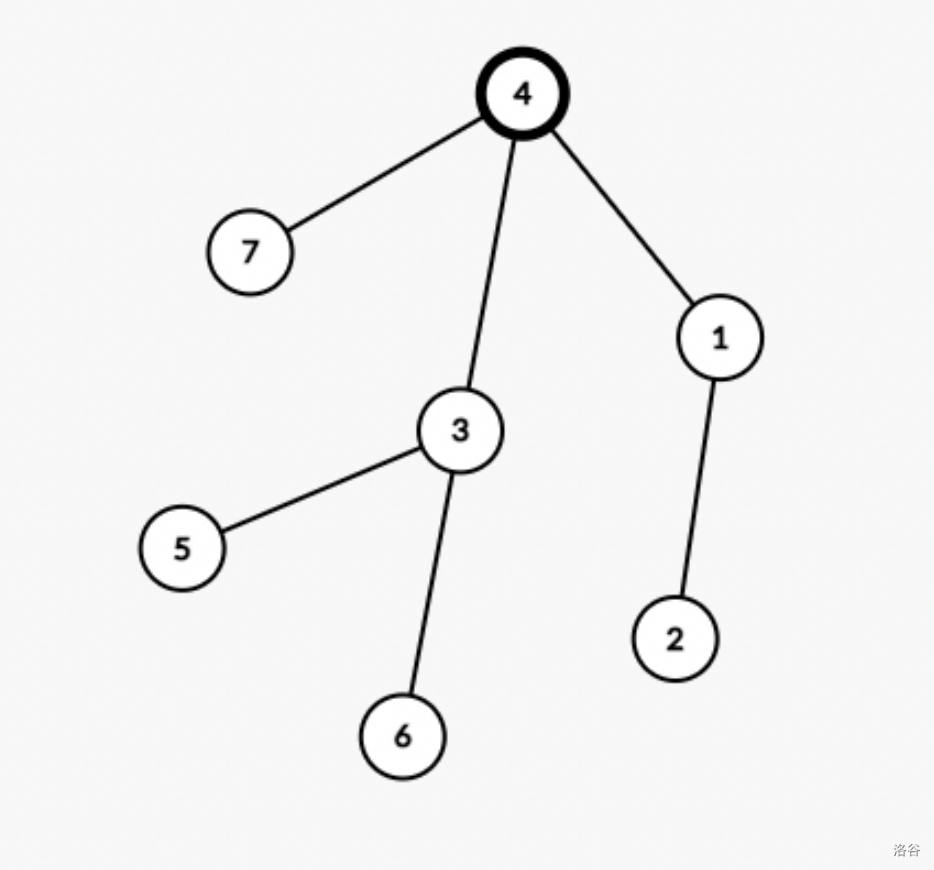
In the first query, the LCA of vertices 5 and 6 is vertex 3 which is not among vertices 5 and 6 so the answer is "NO".

In the second query, the LCA of vertices 3, 5, and 6 is vertex 3 so the answer is "YES".

In the third query, the LCA of vertices 1 and 7 is vertex 4 so the answer is "NO".

In the fourth query, the LCA of vertices 4 and 6 is vertex 4 so the answer is "YES".

After that, we can guess that root is vertex 4 which is the correct answer.

Scoring

1. (7 points): $n \leq 9$
2. (10 points): $n \leq 30$
3. (up to 83 points): $n \leq 500$

In the first and second subtasks you can ask at most 1000 queries.

In the third subtask, let $k$ be the maximum number of queries you asked in any test. If $k \leq 9$, you will get 83 points. Otherwise, you will get $\left\lfloor \max \left(10, 83 \cdot \left(1 - \frac{\ln(k-6)}{7}\right)\right) \right\rfloor$ points.

C++ code that computes the number of points for the third subtask:

((k <= 9) ? 83 : max(10, int(83 * (1 - log(k - 6.0) / 7))))