题目描述

Medea the cat is a real troublemaker. Even though she is loving and caring with humans, sometimes she likes to crash on mouse parties in the field nearby her house, uninvited, just for the fun of it!

:::align{center}

Medea with a mouse.

:::

A mouse party is a bunch of mice standing on the vertices of a convex polygon in the two-dimensional plane. When Medea crashes a mouse party, she jumps, out of nowhere, to some point inside the party's polygon. All the mice and Medea can be considered as points in the two-dimensional plane, meaning that they have no shape or dimensions.

Medea is still careful, however. She considers how the mice might encircle her, so that she runs away before they get a chance to do so. Medea defines an \textit{encirclement} as a subset of exactly three mice such that she lies strictly inside the triangle constructed with the mice as vertices. An example can be seen in Figure M.1.

:::align{center}

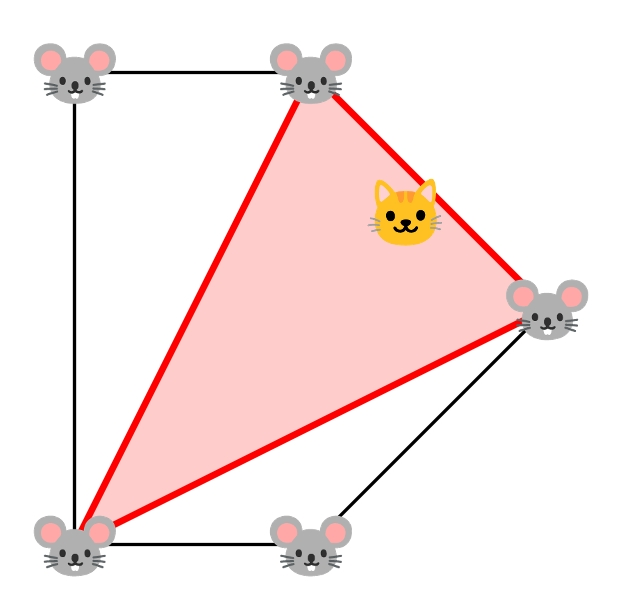
Figure M.1: Illustration of Sample Input 2, showing one of the three encirclements in the case where Medea jumps to $(1.4,1.4)$.

:::

One day, Medea decided to crash on a party of mice. She does not jump accurately, so she does not know exactly which point inside the mouse party she is going to jump to -- all she knows is that she will jump to a uniformly random point with real coordinates inside the mouse party.

Medea wants to know the expected number of distinct encirclements after she lands inside the party. This turned out to be too difficult to calculate, even for Medea's 200 IQ points, so she asked for your help!

输入格式

The input consists of:

• One line with an integer $n$ ($3 \leq n \leq 2\cdot 10^5$), the number of mice.
• $n$ lines, each with two integers $x$ and $y$ ($|x|, |y| \leq 10^7$), the coordinates of a mouse.

The coordinates of the mice are given in counterclockwise order and form a strictly convex polygon with non-zero area. A strictly convex polygon is a convex polygon such that no three consecutive vertices are on a straight line.

输出格式

Output the expected number of encirclements after Medea lands inside the polygon.

Your answer should have an absolute or relative error of at most $10^{-4}$.

4
0 0
1 0
1 1
0 1

2.0

5
0 0
1 0
2 1
1 2
0 2

3.66666667

3
-3141592 -2718281
-3141593 -2718281
-3141592 -2718282

1.0