题目描述

You are given an undirected graph with $n$ vertices and $m$ edges. Each vertex $v$ has a number $a_v$ written on it. This number is either $0$ or $1$. A walk is a sequence $v_1v_2 \dots v_k$ of vertices in the graph such that any two consecutive vertices are connected by an edge. We call a binary sequence

walkable if there is a walk $v_1v_2 \dots v_k$ in the graph that satisfies $a_{v_1} a_{v_2} \dots a_{v_k} = s$.

In other words, a binary sequence is walkable if it is possible to obtain $s$ by walking in the graph and writing down the binary numbers in the order that they are visited. An example is visualized in Figure B.1.

:::align{center}

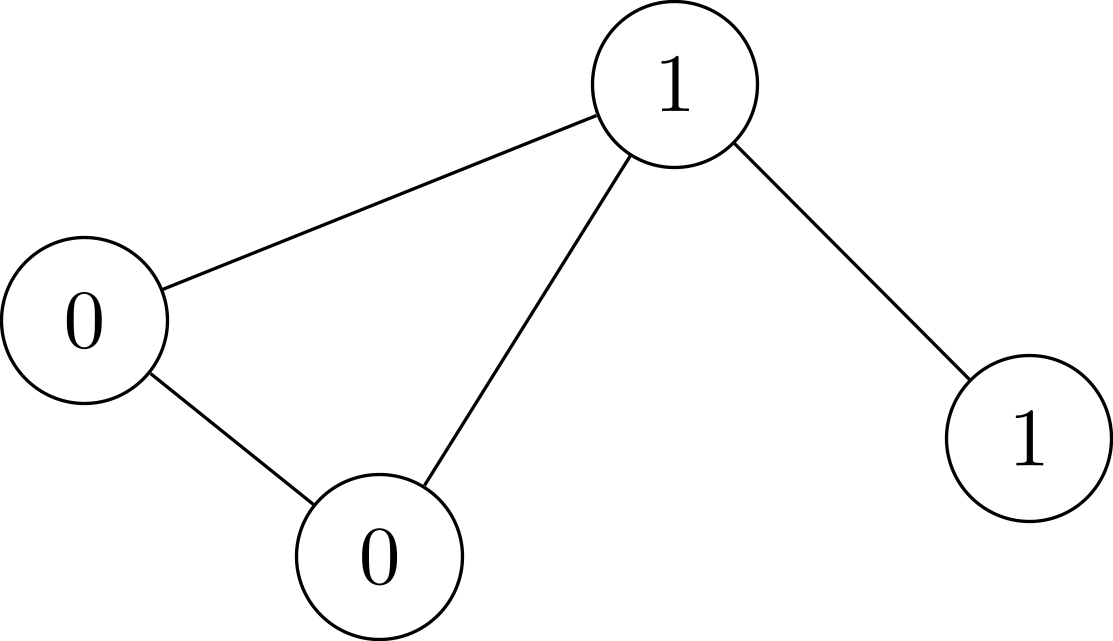
Figure B.1: Illustration of Sample Input 1. Every binary sequence of length at most 3 is walkable. :::

Your task is to find the length of a shortest binary sequence that is not walkable.

输入格式

The input consists of:

• One line with two integers $n$ and $m$ ($1 \leq n \leq 3 \cdot 10^5$, $0 \leq m \leq 3 \cdot 10^5$), the number of vertices and the number of edges.
• One line with $n$ integers $a_1,\dots, a_n$ ($a_v \in \{0, 1\}$ for each $v$), where $a_v$ is the number written on vertex $v$.
• $m$ lines, each with two integers $u$ and $v$ ($1 \leq u,v \leq n$, $u \neq v$), denoting that the vertices $u$ and $v$ are connected by an edge. It is guaranteed that every pair of vertices is connected by at most one edge.

输出格式

If every binary sequence is walkable, output "$\texttt{infinity}$". Otherwise, output the length of a shortest binary sequence that is not walkable.

4 4
0 0 1 1
1 2
1 3
2 3
3 4

4

6 7
0 0 1 1 0 1
1 2
3 1
1 4
2 3
4 2
3 4
5 6

infinity

1 0
0

1