题目背景

Please submit your code in C++20/23.

If all the parts of the ship of Theseus are replaced one by one over time, at what point − if any − does it stop being the same ship?

题目描述

When he's not pondering deeply into the abstract, Theseus slays minotaurs in his spare time. This time however, he must first pass through a dark and twisted labyrinth. Since this is no easy feat, he asks the help of Ariadne to guide him. The labyrinth can be seen as a connected undirected graph with $n$ nodes (labelled from $1$ to $n$) and $m$ edges, with a special node $t$, where the Minotaur sits.

Theseus cannot see the graph at all, but Ariadne can. She and Theseus will devise a strategy so that he can safely reach the node where the Minotaur is: she will put a label with either $0$ or $1$ on each of the $m$ edges. After this, Theseus will enter the labyrinth through a node $s$ that Ariadne doesn't know beforehand.

Since it's very dark, at any moment in time he can only see the index of the node he's in, the indices of neighbouring nodes, and the labels of the adjacent edges. Also, because of the twisted nature of the labyrinth, he can never recall any information regarding previous nodes he has visited.

To reach the Minotaur safely, Theseus must move at most $\min + C$ times, where $\min$ is the minimum number of edges on the path from $s$ to $t$, and $C$ is a constant.

Implementation Details

You will have to implement two functions:

std::vector<int> label(int n, std::vector<std::pair<int,int>> edges, int t);

• $n$: the number of nodes
• $edges$: a list of length $m$ describing the edges of the graph
• $t$: the destination node
• This procedure should return a list of labels of length $m$ where the $i$-th element can be either $0$ or $1$ and it represents the label of the $i$-th edge for all $0 \leq i < m$.
• Every edge must be labelled with either $0$ or $1$. Labelling it with a different label will lead to undefined behaviour.
• This procedure is called exactly once for each test case.

int travel(int n, int u, std::vector<std::pair<int,int>> neighbours);

• $n$: the number of nodes in the graph
• $u$: the current node
• $neighbours$: a list of pairs $(v, e)$ denoting that there is an edge between $u$ and $v$ labelled with $e$
• This procedure should return a neighbouring node to move to. If the neighbouring node is $t$, the program terminates automatically.
• It is guaranteed that for any call to this function, $u$ will not be equal to the special node $t$.
• A call to this procedure represents a move through the labyrinth. Therefore, for each test case, this procedure can be called as many times as necessary in order to reach the destination node.

Attention! The program should not use global/static variables to communicate between different instances of label or travel. Any attempt to circumvent this would lead to undefined behaviour.

提示

Example 1

Consider we have a graph with $7$ nodes and $7$ edges (listed below). The start node will be $3$ (marked with green) and the destination node is $7$ (marked with red). The grader will first call:

label(7, {{1, 6}, {7, 6}, {2, 5}, {3, 2}, {3, 6}, {6, 5}, {6, 4}}, 7)

Let's assume the call to label returns {0, 1, 1, 1, 0, 1, 0}. Then the resulting graph will look like this:

:::align{center} :::

What follows is a possible sequence of calls to travel that will lead to a correct solution:

Call	Returned value
travel(7, 3, {{2, 1}, {6, 0}})	$2$
travel(7, 2, {{5, 1}, {3, 1}})	$5$
travel(7, 5, {{6, 1}, {2, 1}})	$6$
travel(7, 6, {{3, 0}, {5, 1}, {1, 0}, {4, 0}, {7, 1}})	$4$
travel(7, 4, {{6, 0}})	$6$
travel(7, 6, {{3, 0}, {5, 1}, {1, 0}, {4, 0}, {7, 1}})	$7$

When the returned value is $7$ (i.e. the destination), the program stops.

Constraints

• $1 \leq n \leq 10000$
• $1 \leq m \leq 50000$
• $C = 14$
• The start node $s$ is fixed for each test before calling function label.

Subtasks

1. (4 points) The graph is a clique (i.e. there is an edge between any two nodes $1 \leq u < v \leq n$).
2. (10 points) The distance between the destination and any node in the graph is at most 2 edges.
3. (11 points) The graph is a tree.
4. (13 points) The graph is bipartite (i.e. there is a way to divide the nodes of the graph into two subsets such that there is no edge between two nodes from the same subset).
5. (12 points) The graph will be a ladder (see definition below).
6. (50 points) No additional constraints.

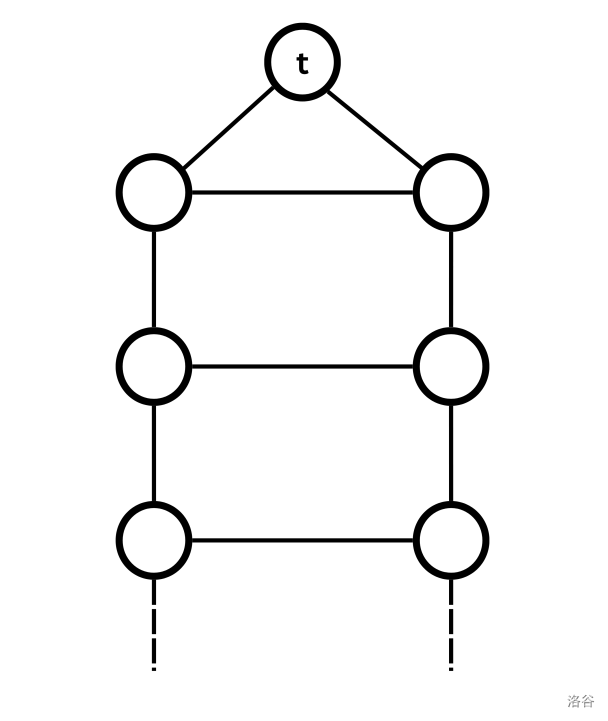
Note: A ladder graph is a graph consisting of two parallel paths (or chains) of the same length, with each pair of corresponding nodes connected by an edge, forming the rungs of the ladder. Additionally, at one end of the ladder, there is a special node – the destination node $t$ – which is connected to both endpoints of the ladder, effectively acting as a common parent. It is guaranteed that $n$ will be odd for any such graph. See the image below.

:::align{center} :::align