题目背景

回忆。

沉溺于过去。

「死期将至」

「惟余旧忆」

回忆。

题目描述

对于一棵有根树，记 $u$ 的子树中除 $u$ 以外的点组成的集合为 $T_u$。

定义点 $u$ 的权值 $f_u=\text{mex}_{v\in T_u}f_v$。特别地，若 $u$ 为叶子，则 $f_u=0$。

现在给定一颗树，每个点 $i$ 除了上述定义的权值外还有一个给定的权重 $a_i$。

这棵树初始只有根结点 $1$，权重为 $a_1$，有 $q$ 次操作，第 $i$ 次输入两个数 $x_i,a_{i+1}$ 代表加入一个新的结点 $i+1$，其权重为 $a_{i+1}$，它的父亲为 $x_i$，求加入这个点之后的 $\sum\limits_{j=1}^{i+1}a_jf_j$。

答案对 $10^9+7$ 取模。

注：每加入一个点后就自叶子结点向根更新 $f$ 的值。

一个集合 $M$ 的 $\operatorname{mex}(M)$ 定义为最小的没有在 $M$ 中出现的自然数。如 $\text{mex}\{1,2,3,4\}=0,\text{mex}\{0,1,3,4\}=2$。

输入格式

第一行两个数 $q,a_1$，接下来接下来 $q$ 行每行两个数 $x_i,a_{i+1}$。

输出格式

输出 $q$ 行，每行一个数，代表加入点 $i+1$ 后所有点的权值乘以权重的和对 $10^9+7$ 取模的结果。

7 2
1 3
1 2
3 1
2 4
5 1
2 3
1 1

2
2
6
9
18
18
18

提示

样例 1 解释

树的形态如图：

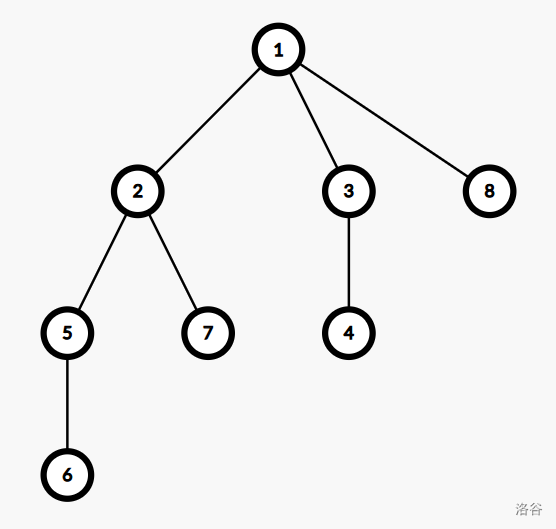
其中各点权值依次为 $3,2,1,0,1,0,0,0$。

举例如对于 $2$ 号点，其子树内点有 $5,6,7$，权值分别为 $1,0,0$，MEX 为 $2$，所以 $2$ 的权值为 $2$。

数据范围

本题 IO 量较大，请尝试使用更快的输入输出方式。

$\text{Subtask}$	子任务依赖	$q\le$	$x_i$	特殊性质	时间限制	分值
$0$	无	$5000$	$x_i\le i$	保证数据随机生成	$1\text s$	$15$
$1$	^	$10^5$	$i-5\le x_i\le i$	无	^	$5$
$2$		^	$x_i\le2$	^		^
$3$			$x_i\le i$	保证数据随机生成		$15$
$4$	$0,1,2,3$		^	无		$20$
$5$	$4$	$10^6$		^		$10$
$6$	$5$	$5\times10^6$			$4\text s$	$30$

对于 $100\%$ 的数据，$1\le q\le5\times10^6,1\le x_i\le i,1\le a_i\le 10^9$。