题目描述

扎克的泽格工效学学位（Zergonomics Zegree）教会了他，在商店里展示物品的最佳方式是把它们堆叠成一种之字形图案。扎克需要将 $n$ 个装有可动人偶的盒子在店门口排成一列。这些盒子可以相互堆叠，并且它们是相同的、不可区分的。他的目标是决定要堆叠成的堆数，然后将盒子堆起来，使得每一堆都不是空的，并且各堆的盒子数量形成一个之字形序列。

形式上，如果有 $s$ ($s \ge 1$) 堆，从左到右编号为 $1$ 到 $s$，且第 $i$ 堆包含 $a_i$ 个盒子，那么必须满足以下条件：

• 对于每个 $i$（从 $1$ 到 $s$），$a_i \ge 1$，
• $a_1 + a_2 + \dots + a_s = n$，并且
• 以下至少一条为真：
  • $a_1 < a_2 > a_3 < a_4 > \dots$，或者
  • $a_1 > a_2 < a_3 > a_4 < \dots$

例如，对于 $n=6$，总共有 $12$ 种方式，如图 M.1 所示。

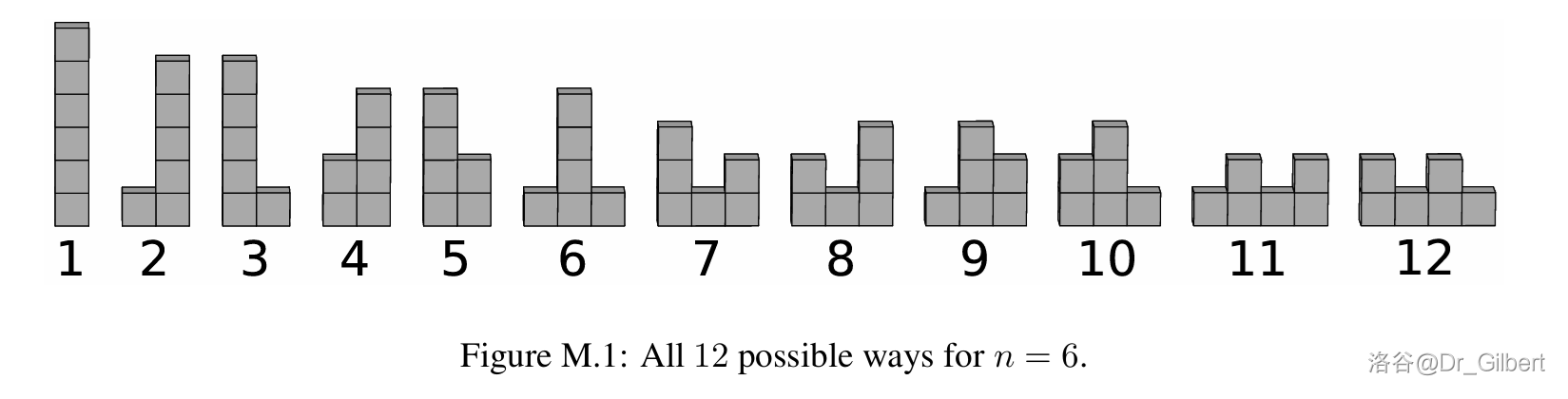
找出扎克可以用多少种不同的方式堆叠这 $n$ 个盒子，结果对 $998,244,353$ 取模。

两种方式被认为是相同的，当且仅当它们的堆数相同，并且在相同位置上的堆所含的盒子数量也相同。

输入格式

输入的第一行包含一个整数 $t$ ($1 \le t \le 300,000$)，代表测试用例的数量。之后是 $t$ 个测试用例。每个测试用例包含一行，内含一个整数 $n$ ($1 \le n \le 300,000$)。

输出格式

对于每个测试用例，输出一个整数，代表堆叠 $n$ 个盒子的不同方式数量，结果对 $998,244,353$ 取模。

4
5
6
7
890

7
12
19
502674609

提示

样例解释 #1

第二个测试用例的 $n$ 值为 $6$，其 $12$ 种方式已在题目描述中说明。