题目描述

亚太地区有 $n$ 个城市，编号从 $1$ 到 $n$。2024 年 ICPC 亚洲及太平洋锦标赛在河内（即城市 $n$）举行。有 $m$ 条双向道路，编号从 $1$ 到 $m$，连接着一些城市对。道路 $i$ 连接城市 $u_i$ 和 $v_i$，任一方向的旅行时间为 $t_i$。每条道路连接不同的城市，且不同的道路连接不同的城市对。

你居住在城市 $1$。你希望通过一系列道路前往城市 $n$ 参加比赛，然后再通过一系列道路返回城市 $1$。走同一条路线很无聊，所以你希望两次行程的路线是不同的。如果两条路线所经过的不同道路的集合是不同的，那么这两条路线就被认为是不同的。

在每次行程中，可以多次经过同一个城市或走同一条道路。在到达目的地城市（即城市 $1$ 或城市 $n$）后，也可以继续行进。行程时间是行程中所经过道路的旅行时间之和。如果一条道路在行程中被多次经过，那么它的旅行时间也会被相应地计算多次。

请确定满足上述要求的两次行程的最小总旅行时间，或者指出无法满足要求。

输入格式

输入的第一行包含两个整数 $n$ 和 $m$ $(2 \le n \le 100,000; 1 \le m \le \min(\frac{n(n-1)}{2}, 300,000)$。

接下来的 $m$ 行，每行包含三个整数。第 $i$ 行包含 $u_i,v_i$ 和 $t_i$ $(1 \le u_i < v_i \le n; 1 \le t_i \le 1000)$。不同的道路连接不同的城市对。

输出格式

输出一个整数，代表满足上述要求的两次行程的最小总旅行时间；如果无法满足要求，则输出 $-1$。

3 2
1 2 10
1 3 5

30

4 3
1 2 10
2 3 5
3 4 2

-1

4 4
1 2 3
2 4 2
1 3 3
3 4 4

12

3 1
1 2 1000

-1

提示

样例解释 #1

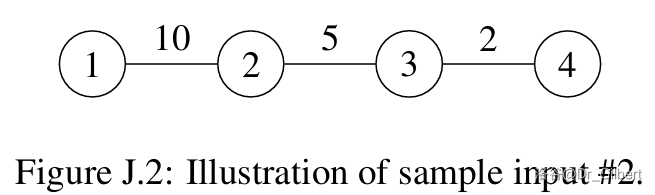
城市和道路如图 J.1 所示。一种可能的最小化总旅行时间的方式如下：

• 从城市 1 前往城市 3，途经道路 2（连接城市 1 和 3）。行程时间为 $5$。经过的道路集合为 $\{2\}$。
• 从城市 3 前往城市 1，途经道路 2，然后两次经过道路 1（连接城市 1 和 2）。行程时间为 $5+10+10=25$。经过的道路集合为 $\{1,2\}$。

可以证明，没有办法以更小的总旅行时间完成两次行程。

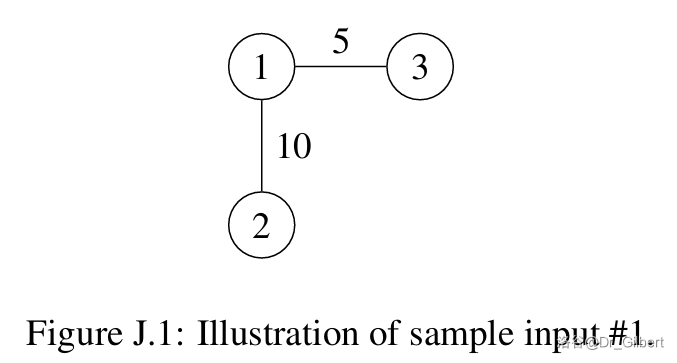
样例解释 #2

城市和道路如图 J.2 所示。从城市 1 前往城市 4 再返回，两次行程都必须经过所有的道路。因此，无法满足上述要求。