题目描述

Eva loves painting. Today she is working with a square canvas of $n \times n$ unit cells. Each cell is painted white, painted black, or empty --- not painted at all.

Eva is going to draw a black triangle inside each empty cell. She wants each triangle to be right-angled and have an area of $\frac{1}{2}$ square unit cells. Thus, there are four ways to draw a single triangle:

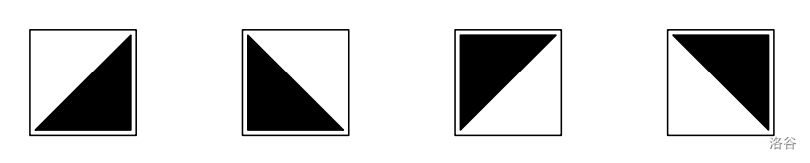
Each triangle is a piece of art, and Eva wants them to be easily distinguishable from the rest of the painting. To achieve that, no two black triangles may share a common side with each other, and no black triangle may share a common side with a black square. Note that two black squares are allowed to share a common side.

Help Eva to find out how many ways there are to finish her painting. Since the number can be large, calculate it modulo $998\,244\,353$.

输入格式

The first line contains a single integer $n$ --- the side length of the canvas ($1 \le n \le 1000$).

The next $n$ lines describe the canvas from top to bottom. The $i$-th of these lines contains $n$ characters $s_{i, 1}, s_{i, 2}, \ldots, s_{i, n}$. If $s_{i, j} =$ $\tt{.}$, the cell in the $i$-th row and the $j$-th column of the canvas is painted white. If $s_{i, j} =$ $\tt{\#}$, that cell is painted black. If $s_{i, j} =$ $\tt{?}$, that cell is empty.

输出格式

Print a single integer denoting the number of ways to finish Eva's painting, modulo $998\,244\,353$.

2
.?
?#

4

3
#??
#??
?##

1

3
.#.
#?#
.#.

0

提示

In the first example test, there are $4$ ways to finish the painting, as illustrated below:

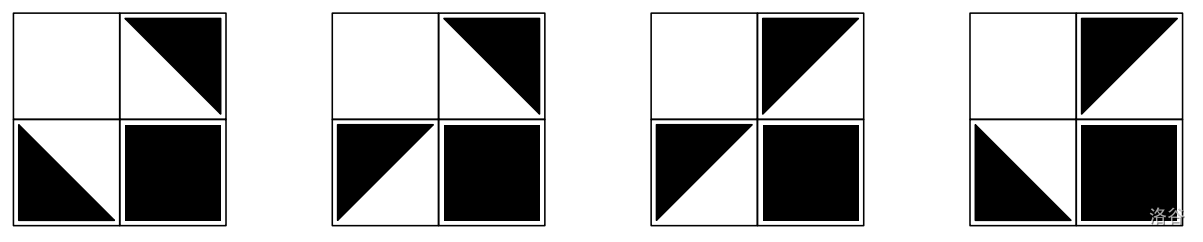
In the second example test, there is a single way to finish the painting:

In the third example test, regardless of how Eva draws the triangle in the center cell, it will share two sides with black squares.