题目描述

After a huge success of the last year's "K-Shaped Figures" problem, we've come up with an innovative "H-Shaped Figures" problem for this year. And we have some plans for the next 24 years.

Let's say that three segments $PQ$, $a$, and $b$ on a plane form an H-shaped figure if:

• point $P$ lies strictly inside segment $a$, and segments $PQ$ and $a$ are not collinear;
• point $Q$ lies strictly inside segment $b$, and segments $PQ$ and $b$ are not collinear;
• segments $a$ and $b$ do not have common points.

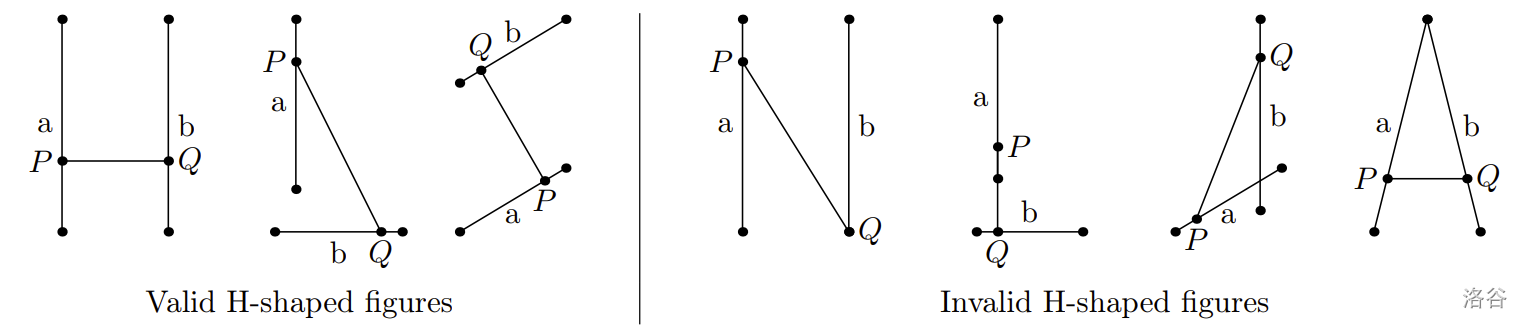
You are given the coordinates of points $P$ and $Q$, along with $n$ candidate segments for $a$ and $b$. Note that some of the given segments may coincide, but they should still be treated as different segments.

Find the number of possible ways to choose one of the given $n$ segments as $a$ and another one as $b$ to form an H-shaped figure along with the given segment $PQ$.

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^5$). The description of the test cases follows.

The first line of each test case contains four integers $x_P, y_P, x_Q, y_Q$, denoting the coordinates of points $P$ and $Q$ ($-10^9 \le x_P, y_P, x_Q, y_Q \le 10^9$). Points $P$ and $Q$ do not coincide.

The second line contains a single integer $n$, denoting the number of candidate segments ($2 \le n \le 2 \cdot 10^5$).

The $i$-th of the following $n$ lines contains four integers $x_{i,1}, y_{i,1}, x_{i,2}, y_{i,2}$, denoting the coordinates of the endpoints of the $i$-th segment ($-10^9 \le x_{i,1}, y_{i,1}, x_{i,2}, y_{i,2} \le 10^9$). All segments have positive lengths.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

输出格式

For each test case, print the number of ways to form an H-shaped figure using the given segment $PQ$ and two of the candidate segments.

1
0 0 4 0
8
0 0 2 1
-1 -1 2 2
3 3 5 -3
0 2 6 -1
2 -2 5 1
-1 1 3 -3
-1 0 2 0
-1 -1 2 2

6