题目背景

小 L 是一只青蛙，他现在准备在 A 城旅行。

题目描述

A 城是一个 $n\times m$ 的矩阵。有一个给定的数 $k$。还有一个变量 $w$，初始为 $0$。记 $(r,c)$ 表示第 $r$ 行第 $c$ 列。

这个矩阵中有 $t$ 个特殊点，第 $i$ 个在 $(x_i,y_i)$，类型为 $p_i$（$p_i\in\{1,2\}$），若 $p_i=2$，则有一个额外属性 $s_i$。保证不存在 $i,j$ 满足 $i\neq j$ 且 $x_i=x_j,y_i=y_j$。

小 L 初始在 $(1,1)$，它可以做任意次以下跳跃方法之一直到它到达 $(n,m)$。假设它现在在 $(a,b)$：

• 选择一个 $h$，满足 $0\le h\le k$，且不存在 $1\le i\le h$ 使得 $(a+i,b)$ 为类型为 $2$ 的特殊点。接着跳到 $(a+h+1,b)$。
• 选择一个 $h$，满足 $0\le h\le k$，且不存在 $1\le i\le h$ 使得 $(a,b+i)$ 为类型为 $2$ 的特殊点。接着跳到 $(a,b+h+1)$。
• 选择一个 $h$，满足 $0\le h\le k$，且不存在 $1\le i\le h$ 使得 $(a+i,b+i)$ 为类型为 $2$ 的特殊点。接着跳到 $(a+h+1,b+h+1)$。

在每次跳跃后，假设跳到了 $(X,Y)$，若 $(X,Y)$ 是第 $Z$ 个特殊点，那么：

• 若 $p_Z=1$，则 $w\leftarrow w+1$。
• 若 $p_Z=2$，令 $w\leftarrow w-s_Z$。

若某个方案中间某个时刻 $w<0$，或某个方案中间某个时刻 $(X,Y)$ 不在矩阵内，则该方案不合法。

问到 $(n,m)$ 的合法方案数，答案对 $10^9+7$ 取模。当且仅当每次的 $(X,Y)$ 组成的序列不同时，两种方案才不同。

输入格式

第一行输入 $4$ 个整数 $n,m,k,t$。

接下来 $t$ 行，每行先输入 $1$ 个整数 $p_i$，然后：

• 若 $p_i=1$，则输入 $2$ 个整数 $x_i,y_i$，表示一个类型为 $1$ 的特殊点。
• 若 $p_i=2$，则输入 $3$ 个整数 $x_i,y_i,s_i$，表示一个类型为 $2$ 的特殊点。

输出格式

第一行输出 $1$ 个整数，表示答案。

3 3 1 2
1 1 3
2 2 3 1

15

3 3 1 0

22

提示

【样例解释 #1】

注：下列每个点代表一个格子；红色箭头为一次跳跃，箭头尾端为 $(X,Y)$；黄色点为 $p_i=1$ 的特殊点；绿色点为 $p_i=2$ 的特殊点。

以下 $15$ 种方案是合法的：

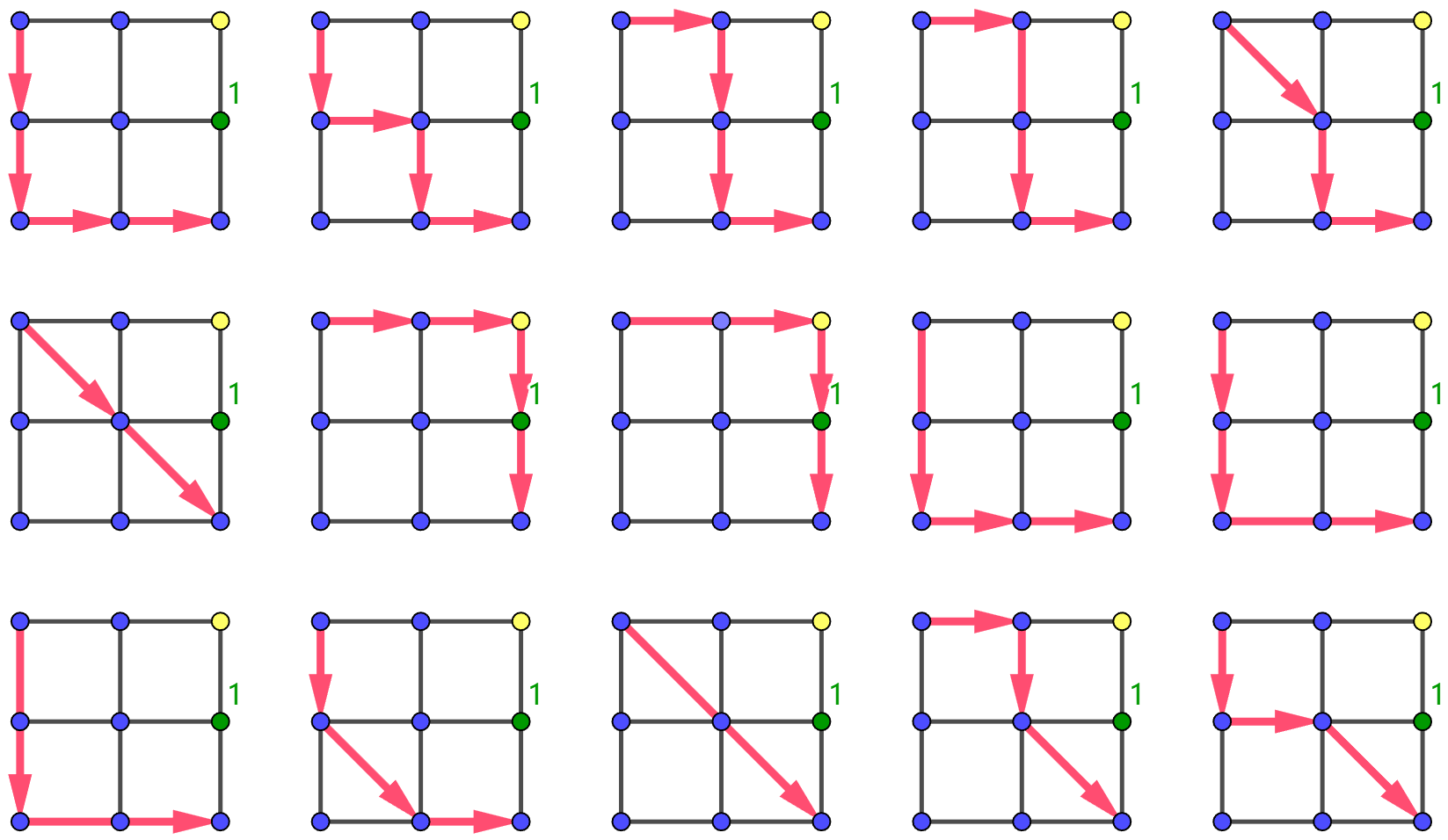
以下 $5$ 种方案不合法，因为在这些方案中，小 L 到 $(2,3)$ 后 $w=-1<0$：

以下 $2$ 种方案不合法，因为在这些方案中，小 L 越过了 $p_i=2$ 的特殊点：

【样例解释 #2】

由于没有特殊点，在样例解释 #1 中展示的合法的 $15$ 种方案，以及不合法的 $7$ 种方案在样例 #2 中均合法，所以答案为 $22$。

【数据范围】

本题采用捆绑测试。

• Subtask #1（$15\text{ pts}$）：$n,m\le8$。
• Subtask #2（$25\text{ pts}$）：$k=0$。
• Subtask #3（$25\text{ pts}$）：$t=0$。
• Subtask #4（$35\text{ pts}$）：无特殊限制。

对于 $100\%$ 的数据，$1\le x_i\le n\le180$，$1\le y_i\le m\le180$，$0\le k\le \max\{n,m\}+1$，$0\le t\le n\times m-2$，$p_i\in\{1,2\}$，$1\le s_i\le356$。

保证没有任何两对 $(x_i,y_i)$ 相同，保证不存在 $(x_i,y_i)=(1,1)$ 或 $(x_i,y_i)=(n,m)$。