题目背景

❤点击链接直达奶龙❤。

题目描述

现有一张 $n$ 个点，初始没有任何边的编号 $1\sim n$ 的图，给定长度为 $m$ 的数组 $A_i$，表示编号为 $A_i$ 的点上有一只奶龙，在每一次行动中，奶龙会沿着当前点连向其它点的边走向下一个点。

请你构造一张图，给定正整数 $k$，使得其满足：

• 每个点的出度均为 $1$，不得有自环。
• 经过恰好 $k$ 次行动时，所有点都被至少一只奶龙经过，且在经过恰好 $k-1$ 次行动时，至少有一个点未被任何奶龙经过。

若无解则输出 -1。

输入格式

第一行共三个整数，表示 $n,m,k$。

第二行共 $m$ 个正整数，其中第 $i$ 个数表示 $A_i$。

输出格式

共 $n$ 行，每行输出两个正整数 $u,v$，表示有一条 $u\to v$ 的有向边。

本题使用 Special Judge，若有多种答案任意输出一种即可。

5 2 2
1 2

1 3
3 5
5 1
2 4
4 5

5 2 1
1 2

-1

提示

样例解释

对于样例组 #1 中的构造方案，图形态如下。

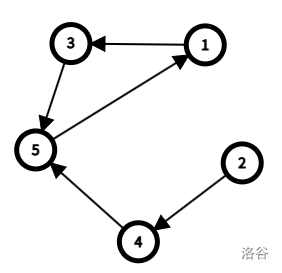
初始点 $1,2$ 上分别有一只奶龙，走第一轮后可以到达 $3,4$，走第二轮后可以到达 $5$，符合题意。

数据范围

子任务编号	$n$	$m$	$k$	分值
$1$	$\le 8$		$< 8$	$10$
$2$	$\le 2\times 10^5$	$=1$	$< 2\times 10^5$	$15$
$3$		$\le 2\times 10^5$	$=1$
$4$			$< 2\times 10^5$	$60$

对于 $100\%$ 的数据，保证 $1\le m\le n\le 2\times 10^5$，$1\le k< n$，$1\le A_i\le n$，$A_i$ 互不相同。另外，为便于编写 Special Judge 保证 $1\le m\times k \le 10^6$，不保证与你的解题过程是否有关。