题目描述

A llama wants to travel through the Andean Plateau. It has a map of the plateau in the form of a grid of $N \times M$ square cells. The rows of the map are numbered from $0$ to $N-1$ from top to bottom, and the columns are numbered from $0$ to $M-1$ from left to right. The cell of the map in row $i$ and column $j$ ($0 \leq i < N$, $0 \leq j < M$) is denoted by $(i, j)$.

The llama has studied the climate of the plateau and discovered that all cells in each row of the map have the same temperature and all cells in each column of the map have the same humidity. The llama has given you two integer arrays $T$ and $H$ of length $N$ and $M$ respectively. Here $T[i]$ ($0 \leq i < N$) indicates the temperature of the cells in row $i$, and $H[j]$ ($0 \leq j < M$) indicates the humidity of the cells in column $j$.

The llama has also studied the flora of the plateau and noticed that a cell $(i, j)$ is free of vegetation if and only if its temperature is greater than its humidity, formally $T[i] > H[j]$.

The llama can travel across the plateau only by following valid paths. A valid path is a sequence of distinct cells that satisfy the following conditions:

• Each pair of consecutive cells in the path shares a common side.
• All cells in the path are free of vegetation.

Your task is to answer $Q$ questions. For each question, you are given four integers: $L$, $R$, $S$, and $D$. You must determine whether there exists a valid path such that:

• The path starts at cell $(0, S)$ and ends at cell $(0, D)$.
• All cells in the path lie within columns $L$ to $R$, inclusive.

It is guaranteed that both $(0, S)$ and $(0, D)$ are free of vegetation.

Implementation Details

The first procedure you should implement is:

void initialize(std::vector<int> T, std::vector<int> H)

• $T$: an array of length $N$ specifying the temperature in each row.
• $H$: an array of length $M$ specifying the humidity in each column.
• This procedure is called exactly once for each test case, before any calls to can_reach.

The second procedure you should implement is:

bool can_reach(int L, int R, int S, int D)

• $L, R, S, D$: integers describing a question.
• This procedure is called $Q$ times for each test case.

This procedure should return true if and only if there exists a valid path from cell $(0, S)$ to cell $(0, D)$, such that all cells in the path lie within columns $L$ to $R$, inclusive.

输入格式

Input format:

N M
T[0] T[1] ... T[N-1]
H[0] H[1] ... H[M-1]
Q
L[0] R[0] S[0] D[0]
L[1] R[1] S[1] D[1]
...
L[Q-1] R[Q-1] S[Q-1] D[Q-1]

Here, $L[k]$, $R[k]$, $S[k]$ and $D[k]$ ($0 \leq k < Q$) specify the parameters for each call to can_reach.

输出格式

Output format:

A[0]
A[1]
...
A[Q-1]

Here, $A[k]$ ($0 \leq k < Q$) is $1$ if the call can_reach(L[k], R[k], S[k], D[k]) returned true, and $0$ otherwise.

提示

Example

Consider the following call:

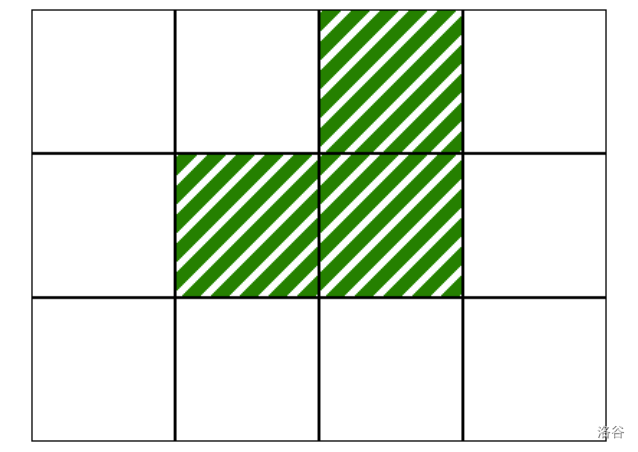
initialize([2, 1, 3], [0, 1, 2, 0])

This corresponds to the map in the following image, where white cells are free of vegetation:

As the first question, consider the following call:

can_reach(0, 3, 1, 3)

This corresponds to the scenario in the following image, where the thick vertical lines indicate the range of columns from $L = 0$ to $R = 3$, and the black disks indicate the starting and ending cells:

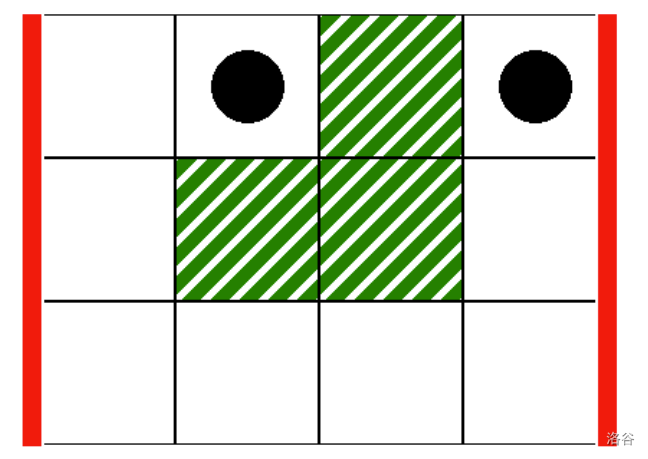
In this case, the llama can reach from cell $(0, 1)$ to cell $(0, 3)$ through the following valid path:

$$(0, 1), (0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (1, 3), (0, 3) $$

Therefore, this call should return true.

As the second question, consider the following call:

can_reach(1, 3, 1, 3)

This corresponds to the scenario in the following image:

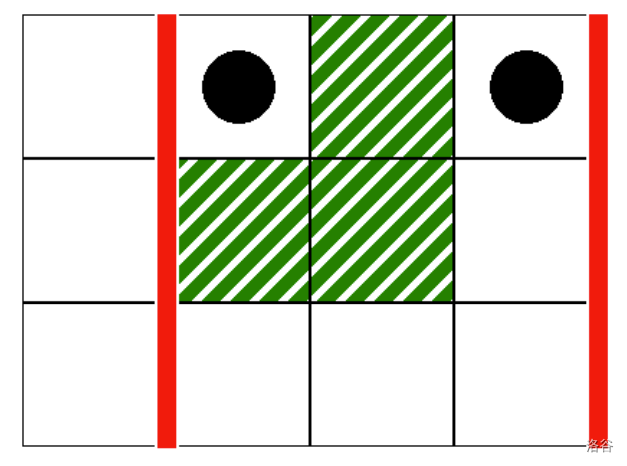
In this case, there is no valid path from cell $(0,1)$ to cell $(0,3)$, such that all cells in the path lie within columns $1$ to $3$, inclusive. Therefore, this call should return false.

Constraints

• $1 \leq N, M, Q \leq 200000$
• $0 \leq T[i] \leq 10^9$ for each $i$ such that $0 \leq i < N$.
• $0 \leq H[j] \leq 10^9$ for each $j$ such that $0 \leq j < M$.
• $0 \leq L \leq R < M$
• $L \leq S \leq R$
• $L \leq D \leq R$
• Both cells $(0, S)$ and $(0, D)$ are free of vegetation.

Subtasks

Subtask	Score	Additional Constraints
1	10	$L = 0, R = M - 1$ for each question. $N = 1$.
2	14	$L = 0, R = M - 1$ for each question. $T[i - 1] \leq T[i]$ for each $i$ such that $1 \leq i < N$.
3	13	$L = 0, R = M - 1$ for each question. $N = 3$ and $T = [2, 1, 3]$.
4	21	$L = 0, R = M - 1$ for each question. $Q \leq 10$.
5	25	$L = 0, R = M - 1$ for each question.
6	17	No additional constraints.