#P13539. [IOI 2025] Migrations
[IOI 2025] Migrations
题目描述
The Natural History Museum is investigating the migration patterns of dinosaurs in Bolivia. Paleontologists have discovered dinosaur footprints at different sites, numbered from to in order of decreasing age: site contains the oldest footprints, while site holds the youngest.
The dinosaurs migrated to each site (except site ) from a specific, older site. For every site such that , there exists exactly one older site (with ) such that some dinosaurs migrated directly from site to site . A single older site may have been the source of migrations to multiple younger sites.
The paleontologists model each migration as an undirected connection between sites and . Note that for any two distinct sites and , it is possible to travel from to by traversing a sequence of connections. The distance between sites and is defined as the minimum number of connections required to travel from to .
For example, the following image displays a case with sites, where , , , and . One can travel from site to site through connections, so the distance between them is .
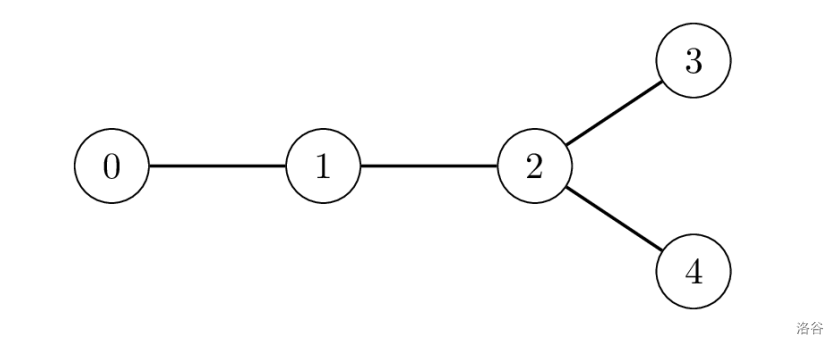
The Museum aims to identify a pair of sites with the maximum possible distance.
Note that the pair is not necessarily unique: for instance, in the example above, both pairs and have a distance of , which is the maximum. In such cases, any of the pairs attaining the maximum distance is considered valid.
Initially, the values of are not known. The Museum sends a research team to visit the sites , in order. Upon reaching each site (), the team performs both of the following actions:
- Determines the value of , that is, the source of migration to site .
- Decides whether to send one message to the Museum or not to send any message from this site, based on the previously gathered information.
Messages are transmitted via an expensive satellite communication system, so each message must be an integer between and , inclusive. Additionally, the team is allowed to send at most messages in total.
Your task is to implement a strategy, through which:
- The research team selects the sites from which messages are sent, along with the value of each message.
- The Museum can determine a pair of sites with the maximum distance, based solely on the messages received from each site, knowing from which sites these messages were sent.
Sending large numbers through the satellite is costly. Your score will depend on both the highest integer sent and the total number of messages transmitted.
Implementation Details
You need to implement two procedures; one for the research team, and another one for the Museum.
The procedure you should implement for the research team is:
int send_message(int N, int i, int Pi)
- : the number of sites with footprints.
- : the index of the site the team is currently visiting.
- : the value of .
- This procedure is called times for each test case, in the order of .
This procedure should return specifying the action taken by the research team at site :
- : the research team decides not to send a message from site .
- : the research team sends the integer as the message from site .
The procedure you should implement for the Museum is:
std::pair<int,int> longest_path(std::vector<int> S)
- : an array of length such that:
- .
- For each , is the integer returned by
send_message(N, i, Pi).
- This procedure is called exactly once for each test case.
This procedure should return a pair of sites with the maximum distance.
In the actual grading, a program that calls the above procedures is run exactly two times.
- During the first run of the program:
- send_message is called exactly times.
- Your program can store and retain information across successive calls.
- The returned values (array ) are stored by the grading system.
- In some cases the behavior of the grader is adaptive. This means that the value of in a call to
send_messagemay depend on the actions taken by the research team during the previous calls.
- During the second run of the program:
longest_pathis called exactly once. The only information available tolongest_pathfrom the first run is the array .
输入格式
The sample grader calls both send_message and longest_path in the same run, which is
different from the actual grader.
Input format:
N
P[1] P[2] ... P[N-1]
输出格式
Output format:
S[1] S[2] ... S[N-1]
U V
Note that you can use the sample grader with any value of .
提示
Example
Let . Consider the situation in which , , , , and for .
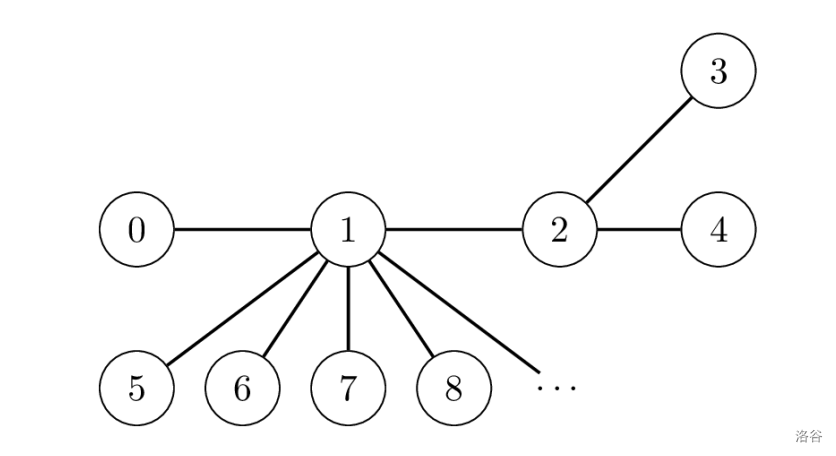
Assume that the research team's strategy is to send the message whenever the pair of sites with the maximum distance changes as a result of a send_message call.
Initially, the pair with the maximum distance is . Consider the following sequence of calls during the first run of the program:
| Procedure call | Return value | |
|---|---|---|
send_message(10000, 1, 0) |
||
send_message(10000, 2, 1) |
||
send_message(10000, 3, 2) |
||
send_message(10000, 4, 2) |
Note that in all the remaining calls the value of is . This means that the pair with the maximum distance does not change, and the team does not send any more messages.
Then, in the second run of the program, the following call is made:
longest_path([0, 10, 20, 30, 0, ...])
The Museum reads the last message sent by the research team, which is , and deduces that is the pair of sites with the maximum distance. Therefore, the call returns .
Note that this approach does not always make it possible for the Museum to determine the pair with the maximum distance correctly.
Subtasks and Scoring
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | 30 | Site 0 and some other site have a maximum distance among all pairs of sites. |
| 2 | 70 | No additional constraints. |
Let be the maximum integer appearing in the array , and let be the number of messages sent by the research team.
In any of the test cases, if at least one of the following conditions hold, then the score of your solution for that test case will be 0 (reported as Output isn't correct in CMS):
- At least one element in is invalid.
- or .
- The return value of the call to procedure longest_path is incorrect.
Otherwise, your score for subtask 1 is calculated as follows:
| Condition | Score |
|---|---|
| 10 | |
| 16 | |
| 23 | |
| 30 |
Your score for subtask 2 is calculated as follows:
| Condition | Score |
|---|---|
| and | |
| and | 40 |
| and | |
| and | 70 |
