#P13537. [IOI 2025] World Map
[IOI 2025] World Map
题目描述
Mr. Pacha, a Bolivian archeologist, discovered an ancient document near Tiwanaku that describes the world during the Tiwanaku Period (300-1000 CE). At that time, there were countries, numbered from 1 to .
In the document, there is a list of different pairs of adjacent countries:
$$\begin{aligned}(A[0], B[0]), (A[1], B[1]), \ldots, (A[M - 1], B[M - 1]).\end{aligned} $$For each (), the document states that country was adjacent to country and vice versa. Pairs of countries not listed were not adjacent.
Mr. Pacha wants to create a map of the world such that all adjacencies between countries are exactly as they were during the Tiwanaku Period. For this purpose, he first chooses a positive integer . Then, he draws the map as a grid of square cells, with rows numbered from 0 to (top to bottom) and columns numbered from 0 to (left to right).
He wants to color each cell of the map using one of colors. The colors are numbered from 1 to , and country () is represented by color . The coloring must satisfy all of the following conditions:
- For each (), there is at least one cell with color .
- For each pair of adjacent countries , there is at least one pair of adjacent cells such that one of them is colored and the other is colored . Two cells are adjacent if they share a side.
- For each pair of adjacent cells with different colors, the countries represented by these two colors were adjacent during the Tiwanaku Period.
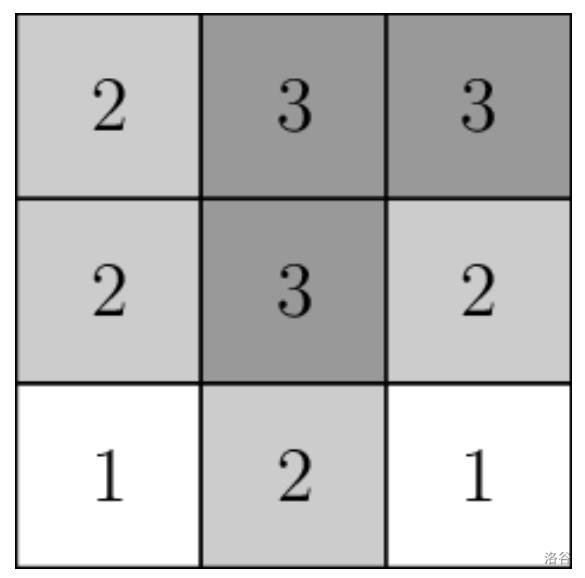
For example, if , and the pairs of adjacent countries are and , then the pair was not adjacent, and the following map of dimension satisfies all the conditions.
:::align{center}
 :::
:::
In particular, a country does not need to form a connected region on the map. In the map above, country 3 forms a connected region, while countries 1 and 2 form disconnected regions.
Your task is to help Mr. Pacha choose a value of and create a map. The document guarantees that such a map exists. Since Mr. Pacha prefers smaller maps, in the last subtask your score depends on the value of , and lower values of may result in a better score. However, finding the minimum possible value of is not required.
Implementation Details
You should implement the following procedure:
std::vector<std::vector<int>> create_map(int N, int M, std::vector<int> A, std::vector<i
- : the number of countries.
- : the number of pairs of adjacent countries.
- and : arrays of length describing adjacent countries.
- This procedure is called up to times for each test case.
The procedure should return an array that represents the map. Let be the length of .
- Each element of must be an array of length , containing integers between and inclusive.
- is the color of the cell at row and column (for each and such that ).
- must be less than or equal to .
输入格式
The first line of the input should contain a single integer , the number of scenarios. A description of scenarios should follow, each in the format specified below.
N M
A[0] B[0]
:
A[M-1] B[M-1]
输出格式
P
Q[0] Q[1] ... Q[P-1]
C[0][0] ... C[0][Q[0]-1]
:
C[P-1][0] ... C[P-1][Q[P-1]-1]
Here, is the length of the array returned by create_map, and () is the length of . Note that line 3 in the output format is intentionally left blank.
2
3 2
1 2
2 3
4 4
1 2
1 3
2 4
3 4
3
3 3 3
2 3 3
2 3 2
1 2 1
7
7 7 7 7 7 7 7
2 1 3 3 4 3 4
2 1 3 3 3 3 3
2 1 1 1 3 4 4
2 2 2 1 3 4 3
1 1 1 2 4 4 4
2 2 1 2 2 4 3
2 2 1 2 2 4 4
提示
Example 1
Consider the following call:
create_map(3, 2, [1, 2], [2, 3])
This is the example from the task description, so the procedure can return the following map.
[
[2, 3, 3],
[2, 3, 2],
[1, 2, 1]
]
Example 2
Consider the following call:
create_map(4, 4, [1, 1, 2, 3], [2, 3, 4, 4])
In this example, , and the country pairs , , , and are adjacent. Consequently, the pairs and are not adjacent.
The procedure can return the following map of dimension , which satisfies all the conditions.
[
[2, 1, 3, 3, 4, 3, 4],
[2, 1, 3, 3, 3, 3, 3],
[2, 1, 1, 1, 3, 4, 4],
[2, 2, 2, 1, 3, 4, 3],
[1, 1, 1, 2, 4, 4, 4],
[2, 2, 1, 2, 2, 4, 3],
[2, 2, 1, 2, 2, 4, 4]
]
The map could be smaller; for example, the procedure can return the following map of dimension .
[
[3, 1],
[4, 2]
]
Note that both maps satisfy .
Constraints
- for each such that .
- The pairs are distinct.
- There exists at least one map which satisfies all the conditions.
Subtasks and Scoring
| Subtask | Score | Additional Constraints |
|---|---|---|
| 1 | 5 | , , for each . |
| 2 | 10 | |
| 3 | 7 | |
| 4 | 8 | Country 1 is adjacent to all other countries. Some other pairs of countries may also be adjacent. |
| 5 | 14 | |
| 6 | 56 | No additional constraints. |
In subtask 6, your score depends on the value of .
- If any map returned by create_map does not satisfy all the conditions, your score for the subtask will be .
- Otherwise, let be the maximum value of over all calls to
create_map. Then, you receive a partial score according to the following table:
| Limits | Score |
|---|---|
