题目背景

CF1801F

题目描述

妈妈给小男孩瓦夏买了一块 $n$ 维巧克力，这块巧克力是一个 $n$ 维立方体，每条边的长度都是 $1$。这块巧克力已经被标出了分割线。在第 $i$ 个维度上，可以用超平面将巧克力沿该维度分成 $a_i$ 份相等的小块。因此，巧克力总共被分成 $a_1 \cdot a_2 \cdot a_3 \cdot \ldots \cdot a_n$ 块，每一小块在第 $i$ 个维度上的长度都是 $\frac{1}{a_i}$，因此每一小块的体积为 $\frac{1}{a_1 a_2 \cdots a_n}$。

瓦夏和他的朋友们想要把巧克力切成至少 $k$ 块，并且希望最小的那一块的体积尽可能大。巧克力只能在原本小块的连接处切割，每一次切割都必须是沿着参与形成小块的某个超平面，且每次切割都要贯穿整个巧克力。所有切割都完成后，瓦夏才将巧克力分成小块。

更正式地说，瓦夏需要选择 $b_1, b_2, \dots, b_n$ 这 $n$ 个数（$1 \le b_i \le a_i$），表示在第 $i$ 个维度上将巧克力切成 $b_i$ 份。需要满足 $b_1 \cdot b_2 \cdot \ldots \cdot b_n \ge k$，这样切割后才能得到不少于 $k$ 块巧克力。可以注意到，在最优切割方案下，最小的一块包含 $\lfloor \frac{a_1}{b_1} \rfloor \dotsm \lfloor \frac{a_n}{b_n} \rfloor$ 个小块，其体积为 $\lfloor \frac{a_1}{b_1} \rfloor \dotsm \lfloor \frac{a_n}{b_n} \rfloor \cdot \frac{1}{a_1 a_2 \cdots a_n}$。

瓦夏希望得到的答案是：最小一块体积的最大可能值乘以 $k$，也就是最大化 $\lfloor \frac{a_1}{b_1} \rfloor \dotsm \lfloor \frac{a_n}{b_n} \rfloor \cdot \frac{1}{a_1 a_2 \cdots a_n} \cdot k$。请你帮他实现这个目标。

输入格式

第一行包含两个整数 $n$ 和 $k$（$1 \le n \le 100$，$1 \le k \le 10^7$），分别表示巧克力的维度和需要分成的块数。

第二行包含 $n$ 个整数 $a_1,\ a_2,\ \dots,\ a_n$（$1 \le a_i \le 10^7$），表示在每个维度上巧克力被分成的小块数。

输出格式

输出一个数，表示最大可能的“最小块体积乘以 $k$”，结果的绝对或相对误差不超过 $10^{-9}$。

如果在给定限制下无法将巧克力分成至少 $k$ 块，输出 $0$。

1 2
5

0.8

2 6
5 10

0.72

2 7
4 4

0.875

2 3
4 5

0.75

4 444
57 179 239 2

0.97557326850704739751

2 5
2 2

0

提示

样例解释

在第一个样例中，一维的巧克力可以这样切割：

:::align{center} :::

此时答案为 $\frac{2}{5} \cdot 2 = 0.8$。

在第二个样例中，巧克力可以这样切割：

:::align{center} :::

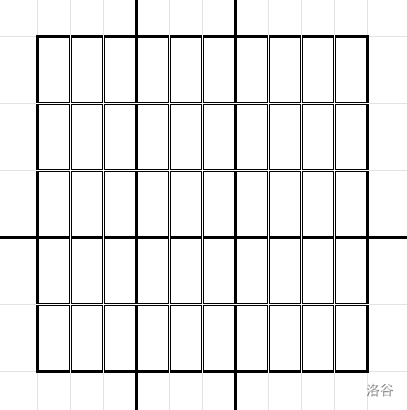此时答案为 $\frac{2}{5} \cdot \frac{3}{10} \cdot 6 = 0.72$。

在第三个样例中，巧克力可以这样切割：

:::align{center} :::

此时答案为 $\frac{2}{4} \cdot \frac{1}{4} \cdot 7 = 0.875$。

评分说明

本题的测试数据分为 8 组。只有通过某一组的全部测试点，且通过部分之前组的全部测试点后，才能获得该组的分数。注意，有些分组不需要通过样例中的测试点。“离线评测”表示该组的测试结果只会在比赛结束后公布。

组别	分值	$n$	$k$	$a_i$	必须通过的组	备注
0		--	--			样例测试点
1	10	$n \le 2$
2	12	--	$k \le 500$	$a_i \le 500$	0
3	13		$k \le 20\,000$	$a_i \le 2000$	0, 2
4	12		$k \le 40\,000$	--	0, 2, 3
5	10		$k \le 200\,000$		0, 2, 3, 4
6	11		$k \le 4 \cdot 10^6$	$a_i \le 2000$	0, 2, 3
7	15		$k \le 5 \cdot 10^6$	--	0, 2 -- 6
8	17		--		0 -- 7	离线评测