题目背景

试题来源：https://koi.or.kr/archives/。中文翻译做了少量本土化修改。

按照署名—非商业性使用—相同方式共享 4.0 协议国际版进行授权。

题目描述

对于 $N \ge 2$ 的情况，有 $N$ 个编号从 1 到 $N$ 的顶点按顺序排列在一条直线上，对于每个 $i$ ($1 \le i \le N-1$)，都有一条双向连接顶点 $i$ 和 $i+1$ 的边。

例如，在 $N=5$ 的情况下，顶点和边的排列如下图所示。

:::align{center} :::

小郑可以在这个图上通过跳跃来移动。当小郑从一个顶点跳跃到另一个顶点时，他会经过它们之间的所有边各一次。

例如：

• 如果小郑从顶点 4 跳到顶点 2，他会分别经过顶点 3 和 4 之间的边，以及顶点 2 和 3 之间的边各一次。
• 如果小郑从顶点 3 跳到顶点 4，他会经过顶点 3 和 4 之间的边一次。

小郑从顶点 1 开始，经过 $N-1$ 次跳跃后到达顶点 $N$，在此过程中，他恰好访问了每个顶点一次。（最初在顶点 1 也算作一次访问。）

换句话说，如果将小郑访问顶点的顺序记为 $p_1 \rightarrow p_2 \rightarrow \cdots \rightarrow p_{N-1} \rightarrow p_N$，则 $p_1 = 1$，$p_N = N$，并且 $\{p_1, p_2, \ldots, p_N\} = \{1, 2, \ldots, N\}$。

此时，将小郑在跳跃过程中经过顶点 $i$ 和 $i+1$ 之间的边的总次数记为 $c_i$ ($1 \le i \le N-1$)。

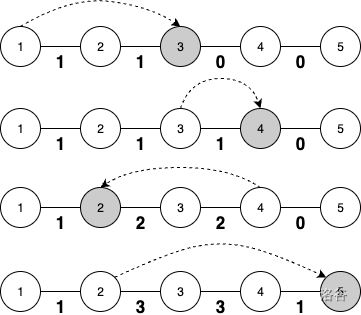
例如，如果小郑按 $(p_1 = 1) \rightarrow (p_2 = 3) \rightarrow (p_3 = 4) \rightarrow (p_4 = 2) \rightarrow (p_5 = 5)$ 的顺序访问，则 $c_1 = 1, c_2 = 3, c_3 = 3, c_4 = 1$。

:::align{center} :::

当给定小郑访问顶点时经过各条边的次数所构成的序列 $c = (c_1, c_2, \ldots, c_{N-1})$ 时，请编写一个程序，根据此序列求出小郑的访问顺序 $p_1, p_2, \ldots, p_N$。

给定的序列 $c$ 总是由某个访问顺序生成的，因此满足条件的访问顺序总是存在的。如果存在多个可能的访问顺序，输出任意一个即可。

输入格式

第一行给定顶点的数量 $N$。

第二行给定 $N-1$ 个整数 $c_1, c_2, \ldots, c_{N-1}$，以空格分隔。此时，$c_i$ 表示经过顶点 $i$ 和 $i+1$ 之间边的次数。

输出格式

输出小郑的可能访问顺序 $p_1, p_2, \ldots, p_N$，以空格分隔。如果存在多个可能的访问顺序，输出任意一个即可。

5
1 3 3 1

1 3 4 2 5

7
1 3 3 5 3 1

1 6 2 3 5 4 7

提示

限制条件

• 所有给定的数都是整数。
• $2 \le N \le 200\,000$
• 对于所有满足 $1 \le i \le N-1$ 的 $i$，有 $1 \le c_i \le 10^{18}$。
• 输入保证存在可能的访问顺序。

子任务

1. (10 分) $N \le 10$。
2. (10 分) 对于所有满足 $1 \le i \le N-1$ 的 $i$，有 $c_i \le 3$。
3. (15 分) $N \ge 4$，且存在一个整数 $M$ ($2 \le M \le N-2$)，使得 $c_1 \le c_2 \le \cdots \le c_M$ 并且 $c_M \ge c_{M+1} \ge \cdots \ge c_{N-1}$。换句话说，$c_i$ 的序列呈现先单调递增后单调递减的形态。
4. (35 分) $N \le 300$。
5. (30 分) 无额外限制条件。