题目背景

试题来源：https://koi.or.kr/archives/。中文翻译做了少量本土化修改。

按照署名—非商业性使用—相同方式共享 4.0 协议国际版进行授权。

题目描述

小郑想要在仓库里存放箱子。总共有 $N$ 个箱子，编号从 1 到 $N$。第 $i$ ($1 \le i \le N$) 号箱子的大小为 $s_i$，收纳容量为 $c_i$。所有箱子的收纳容量都比其自身的大小要小，即满足 $c_i < s_i$。

小郑觉得仓库里的箱子太多、太杂乱，因此想把一些箱子装到另一些箱子里来存放。此时，必须满足以下条件：

• 一个箱子可以装下大小不大于其收纳容量的箱子。
• 已经装有其他箱子的箱子，也可以被装入另一个箱子中。
• 一个箱子直接容纳的箱子最多只能有一个。换句话说，一个箱子内最多可以直接放入一个其他的箱子，但允许这个被放入的箱子内部还装有别的箱子。

存放箱子的成本，等于没有被装在任何其他箱子里的箱子的数量。

例如，假设 $N = 4$，四个箱子的大小和收纳容量分别如下表所示。

编号	大小	收纳容量
1	6	4
2	5	1
3	9	8
4	2	1

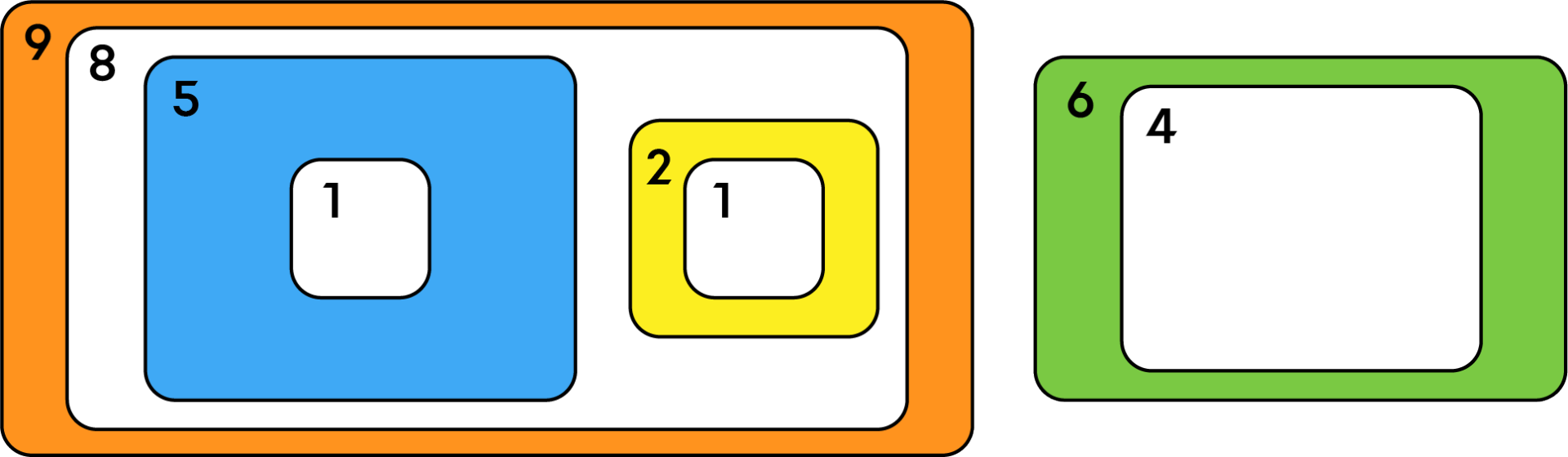
此时，如下图所示，如果将 4 号箱子放入 1 号箱子，再将 1 号箱子放入 3 号箱子，那么没有被装在其他箱子里的箱子就有 2 个 (3 号箱子和 2 号箱子)，因此存放箱子的成本为 2。

但是，如下图所示，如果将 2 号箱子和 4 号箱子都放入 3 号箱子中，由于 3 号箱子内直接容纳了两个箱子，因此不满足条件。

仓库里不必非要放下所有的箱子，所以小郑计划只保留编号较小的一部分箱子，并丢弃其余的。小郑目前还没有决定要使用多少个箱子。

请你帮助小郑，对于从 1 到 $N$ 的所有 $i$，编写一个程序来计算存放 $1, 2, \ldots, i$ 号箱子所需的最小成本。

输入格式

第一行给定箱子的数量 $N$。

从第二行开始的 $N$ 行，给出了各个箱子的信息。其中第 $i$ 行（指这 $N$ 行中的第 $i$ 行，即文件的第 $i+1$ 行）是关于第 $i$ 号箱子的，给出了其大小 $s_i$ 和收纳容量 $c_i$，以空格分隔。

输出格式

输出 $N$ 行。

第 $i$ ($1 \le i \le N$) 行输出存放 $1, 2, \ldots, i$ 号箱子所需的最小成本。

4
6 4
5 1
9 8
2 1

1
2
2
2

6
3 2
5 4
3 2
4 3
4 3
3 2

1
1
2
2
2
3

8
13 6
7 5
9 4
11 10
4 2
15 5
16 7
8 3

1
2
3
3
3
4
4
5

提示

限制条件

• 所有给定的数都是整数。
• $2 \le N \le 2 \times 10^5$
• $1 \le c_i < s_i \le 10^9$ ($1 \le i \le N$)

子任务

1. (7 分) $N \le 6$。
2. (12 分) 对于所有 $i$，$s_i = c_i + 1$。
3. (26 分) $N \le 1000$。
4. (17 分) 对于所有 $i$，$s_i \le 100$。
5. (38 分) 无额外限制条件。