题目描述

Once upon a time, the princess of Burlyandia, Burenka, decided to please her friend ReLu. Knowing that ReLu shares her interest in cryptocurrency, Burenka decided to create her own blockchain cryptocurrency called $\texttt{Pether}$.

After taking courses and training from an expert coach in personal growth in cybersecurity, Burenka decided that the currency $\texttt{Pether}$ should be protected in the best possible way. As a result, due to incredibly complex and convoluted restrictions, not all users can exchange $\texttt{Pether}$ with each other.

The structure of the $\texttt{Pether}$ blockchain currency is indeed complex and convoluted. All users are numbered with integers from $1$ to $n$. Each user is assigned a $\textbf{unique}$ identifier $a_{i}$. Also, the currency has a security parameter $d$.

User $i$ can directly transfer currency to user $j$ only if $i < j$ and $a_i < a_j$. But that's not enough! Direct currency transfer between users occurs through a chain of transactions involving some number of intermediate users. During each transaction, the number of each subsequent intermediate user (including the last user $j$) must increase, but not by more than $d$. Also, all intermediate users except $i$ and $j$ must have an identifier strictly less than $a_i$.

More formally, user $i$ can directly transfer cryptocurrency to user $j$ if the following conditions are met:

• It is satisfied that $i < j$
• It is satisfied that $a_{i} < a_{j}$
• There exists a sequence of intermediate users $x$ of length $k$ such that:
  • $i = x_1 < x_2 < \ldots < x_{k-1} < x_{k} = j$
  • For all $1 \le t \le k - 1$, it is true that $x_{t + 1} - x_{t} \le d$
  • For all $2 \le t \le k - 1$, it is true that $a_{x_t} < a_{i}$

Burenka asks you, her acquaintance programmer, to understand this system and find out for some pairs of users how to transfer $\texttt{Pether}$ to each other.

You need to answer $q$ queries. In each query, you need to determine whether there is a sequence of direct currency transfers (possibly through intermediate users) that allows transferring $\texttt{Pether}$ from user $u_i$ to user $v_i$. In some queries, it is also necessary to minimize the number of direct currency transfers in the process of sending currency from $u_i$ to $v_i$. Please note that it is not necessary to minimize the number of transactions during each direct transfer.

输入格式

The first line contains three integers $n$, $d$, and $g$ $(1 \leq n, d \leq 300\,000, 0 \leq g \leq 12)$ --- the number of users, the security parameter, and the test group number.

The second line contains $n$ integers $a_1,\ a_2,\ \ldots,\ a_n$ $(1 \leq a_{i} \leq n)$ --- user identifiers. It is guaranteed that all numbers $a_i$ are $\textbf{distinct}$.

The third line contains a single integer $q$ $(1 \leq q \leq 300\,000)$ --- the number of queries.

The next $q$ lines contain three integers each $t_{i},\ u_{i},\ v_{i}$ $(t_{i}\in \{1, 2\}, 1 \leq u_{i} < v_{i} \leq n)$, where $u_i$ is the user who should transfer the currency, and $v_i$ is the user who should receive the currency. If $t_i = 1$, then it is necessary to determine whether it is possible to transfer the currency, and if $t_i = 2$, then it is also necessary to minimize the number of direct currency transfers.

输出格式

Output $q$ lines, where the $i$-th line should contain the answer to the $i$-th query.

If it is not possible to transfer the currency from user $u_i$ to user $v_i$, then output 0 as the answer to the $i$-th query. Otherwise, if $t_i = 1$, output 1, and if $t_i = 2$, output the minimum number of direct currency transfers required to transfer $\texttt{Pether}$ from $u_i$ to $v_i$.

6 1 0
2 1 3 4 5 6
6
2 1 3
2 1 2
1 1 4
2 1 5
2 1 6
1 2 6

1
0
1
3
4
1

6 2 0
1 2 3 4 5 6
6
2 1 5
2 2 5
2 1 6
2 2 6
2 1 4
2 2 4

2
2
3
2
2
1

10 2 0
2 1 4 3 5 6 8 7 10 9
10
2 1 5
1 2 5
2 3 5
2 1 9
2 5 8
2 3 9
2 1 8
1 1 2
2 3 8
2 1 9

2
1
1
4
2
3
3
0
2
4

提示

Note

In the first example, the following direct transfers between users are possible:

In the first query, user with index $1$ can directly transfer $\texttt{Pether}$ to user with index $3$, making 2 transactions through intermediate user 2.

In the second query, a direct transfer between users with indices $1$ and $2$ is not possible, as $a_{1} = 2 > a_{2} = 1$.

In the third query, it is possible to transfer the currency from user $1$ to user $4$ with two direct transfers, first transferring the currency from user $1$ to user $3$, and then from $3$ to $4$. Since $t_3 = 1$, it is only necessary to determine the possibility of transferring the currency, so the answer to the query is 1.

In the fourth query, it is possible to manage with three direct transfers: from $1$ to $3$, from $3$ to $4$, and from $4$ to $5$.

In the second example, the following direct transfers between users are possible:

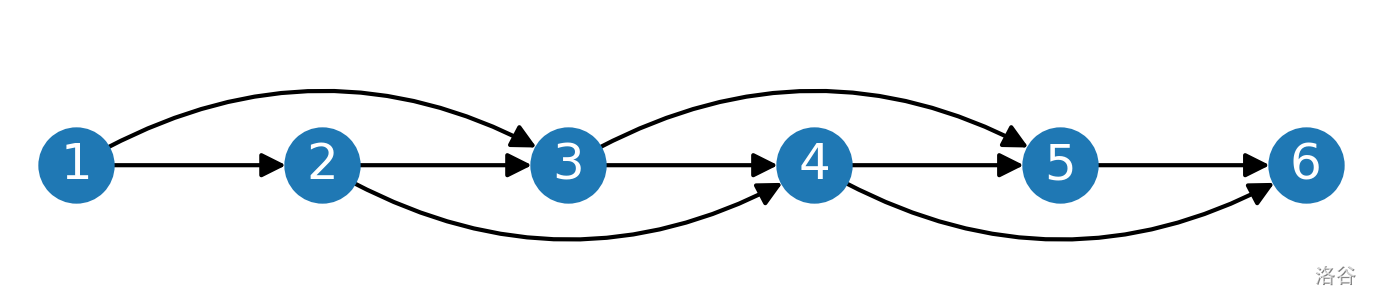
In the third example, the following direct transfers between users are possible:

Scoring

The tests for this problem consist of twelve groups. Points for each group are given only if all tests of the group and all tests of the required groups are passed. Please note that passing the example tests is not required for some groups. $\textbf{Offline-evaluation}$ means that the results of testing your solution on this group will only be available after the end of the competition.

Group	Points	Additional constraints	<		Required groups	Comment
		$n$	$q$	$v_i, a_n, t_i$
0		--		--	--	Examples.
1	10	$n \le 100$	$q \le 100$
2	7	$n \le 1000$	--		1
3	14	--		$a_n = n, v_i = n$	--
4	10		$q = 1$	$v_i = n$
5	9		--		3, 4
6	7			$t_i=2$	--	The answer does not exceed $10$
7					1, 6	The answer does not exceed $150$
8	13			$t_i = 1$	--
9	10	$n \le 50\,000$	$q \le 50\,000$	--	1
10	4	$n \le 100\,000$	$q \le 100\,000$		1, 9
11		$n \le 200\,000$	$q \le 200\,000$		1, 9, 10
12	5	--			0--11	Offline-evaluation.