题目描述

Volodya dreams of becoming a detective. Therefore, Volodya often reads books that tell incredible stories of solving crimes. Studying the next case, Volodya came across interesting details of the investigation.

There were a total of $n$ suspected persons in the case. The evidence board contains all $n$ persons. Initially, there were no connections between them.

During the investigation, new connections between suspected persons emerged one after another. Each connection linked two persons that previously had no connection with each other, even indirectly through several other persons.

Let's consider what happened when a connection between persons $A$ and $B$ emerged. In addition to the names of the persons, each connection had three parameters: $c_A$ --- the strength of the evidence against $A$, $c_B$ --- the strength of the evidence against $B$, and $w_{AB}$ --- the total strength of the evidence of connection. For natural reasons, the strength of the evidence of connection could not exceed the sum of strengths of the evidence against $A$ and $B$. That means that for each connection, it was $\textbf{necessarily}$ that $w_{AB} \leq c_A + c_B$. Upon receiving such connection, the detectives drew a line on the board between the images of persons $A$ and $B$, assigning the $w_{AB}$ to this line. Also, a sticker with the number $c_A$ was placed on the image of person $A$, and a sticker with the number $c_B$ was placed on $B$. If there were already other stickers on the image, the new sticker was placed on top of the old ones.

The case was solved exactly at the moment when all the suspected persons were linked through $n-1$ connections. After solving the crime, the board was placed in the museum in its original form.

Inspired by this approach, Volodya visited that museum and studied the evidence board in detail. Volodya noticed that the image of person $v$ contained stickers with numbers $c_{v,1}, \ldots, c_{v,deg_v}$ numbered $\textbf{from top to bottom}$. Here, $deg_v$ denotes the number of connections associated with person $v$. Also, Volodya remembered that the $i$-th connection was between persons $a_i$ and $b_i$ and had evidence strength $w_i$. Unfortunately the connections were arbitrarily numbered, and their numbers did not necessarily correspond to the order in which they appeared during the investigation.

Due to the confusion with the numbers of connections, the information on the board did not help to restore the process of the investigation. Now Volodya needs to restore any possible chronological order in which the connections could have emerged for the detectives. This task is too difficult for him, so he asks your help. It is also possible that the museum falsified information, and a suitable order does not exist.

输入格式

The first line of the input contains two integers $n$ and $g$ ($2 \le n \le 200\,000$, $0 \le g \le 9$) --- the number of suspected persons in the case and the test group number.

The next $n - 1$ lines describe the connections. The $i$-th line contains three integers $a_i$, $b_i$, and $w_i$ ($1 \le a_i, b_i \le n$, $1 \le w_i \le 10^9$, $a_i \neq b_i$) --- the persons connected by the $i$-th connection and the total strength of the $i$-th connection. It is guaranteed that connections link all persons together.

The next $n$ lines describe the numbers written on the stickers. The $i$-th line contains $deg_i$ integers $c_{i, 1}, \ldots, c_{i, deg_i}$ ($0 \le c_{i, j} \le 10^9$) --- the numbers written on the stickers on the image of the $i$-th person from top to bottom. $deg_i$ equals the number of connections associated with person $i$.

输出格式

If there is no suitable chronological order for the restoration of connections according to the conditions of the problem, output $\tt{No}$ (without quotes) on a single line.

Otherwise, on the first line output $\tt{Yes}$ (without quotes). On the second line, output $n - 1$ numbers --- a suitable chronological order of connections to emerge. The connections are numbered from $1$ to $n-1$ in the same order as they are given in the input. If there are multiple possible orders, output any of them.

5 0
1 2 3
1 3 1
3 4 12
3 5 6
0 4
2
6 1 3
8
3

Yes
1 4 2 3

7 0
1 2 4
2 3 4
3 4 4
4 5 4
5 6 4
6 7 4
2
1 2
2 3
1 2
3 2
1 2
179

Yes
5 1 2 3 6 4

4 0
1 2 7
1 3 6
1 4 5
3 2 1
5
4
3

No

提示

Note

In the first example, one of the possible orders is $[1, 4, 2, 3]$. In chronological order, the first connection links $A = 1$ and $B = 2$, $c_A = 4, c_B = 2, w_{AB} = 3$, $3 \leq 2 + 4$ --- the evidence is correct. The second connection links $A = 3$ and $B = 5$, $c_A = 3, c_B = 3, w_{AB} = 6$, $6 \leq 3 + 3$ --- the evidence is correct. The third connection links $A = 1$ and $B = 3$, $c_A = 0, c_B = 1, w_{AB} = 1$, $1 \leq 0 + 1$ --- the evidence is correct. The fourth connection links $A = 3$ and $B = 4$, $c_A = 6, c_B = 8, w_{AB} = 12$, $12 \leq 6 + 8$ -- the evidence is correct. For a better understanding, refer to the illustration.

:::align{center} :::

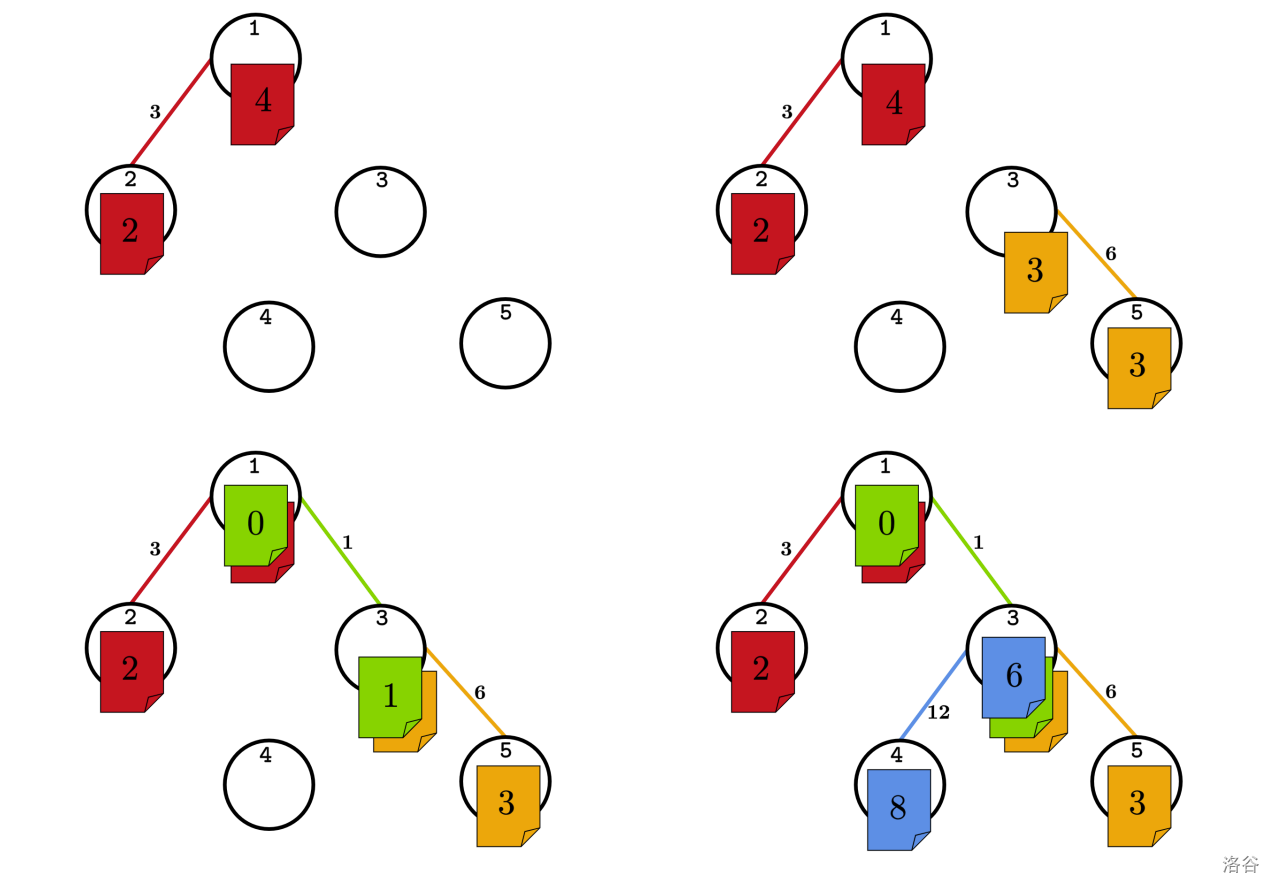Scoring

The tests for this problem consist of nine groups. Points for each group are given only if all tests of the group and all tests of the required groups are passed. Please note that passing the example tests is not required for some groups. $\textbf{Offline-evaluation}$ means that the results of testing your solution on this group will only be available after the end of the competition.

Group	Points	Additional constraints	<	Required Groups	Comment
		$n$	$a_i, b_i, c_i, w_i$
0		--	--	--	Examples.
1	10	$n \le 10$		0	--
2	15	--	$a_i = i, b_i = i+1$ for all $i$	--
3	8		$a_i = 1, b_i = i+1$ for all $i$
4	9		$a_i \leq 2, b_i = i+1$ for all $i$	3
5	7	$n \le 1000$	$c_{i,1} \leq c_{i,2} \leq \ldots \leq c_{i, deg_i}$ for all $i$	--
6			$c_{i, j} = 0$ for all $1 \le i \le n$ and $j \geq 2$
7	17	--	$\displaystyle\sum_{v=1}^{n} \displaystyle\sum_{i=1}^{deg_v} c_{v,i} = \displaystyle\sum_{i=1}^{n-1} w_i$
8	16	$n \le 1000$	--	0, 1, 5, 6
9	11	--		0 -- 8	Offline-evaluation