题目描述

This is an interactive problem.

You are given $n$ points $A_i = (x_i, y_i)$ on the plane. It is known that all $x_i$ are distinct and all $y_i$ are distinct.

Your task is to draw polygonal lines connecting these $n$ points.

A polygonal line is defined by a permutation $p_1, p_2, \ldots, p_n$ of numbers from $1$ to $n$. The polygonal line consists of $n-1$ segments, the first segment connects points $A_{p_1}$ and $A_{p_2}$, the second segment connects points $A_{p_2}$ and $A_{p_3}$, $\ldots$, the last segment connects points $A_{p_{n-1}}$ and $A_{p_n}$. Note that segments may intersect.

The $\textit{sharpness}$ of a polygonal line is defined as the number of indices $2 \leq i \leq n - 1$ such that the angle $\angle A_{p_{i-1}} A_{p_i} A_{p_{i+1}}$ is acute, i.e., strictly less than $90^{\circ}$.

You need to solve four tasks:

• Find any polygonal line that has the maximum possible sharpness.
• Given an integer $c$. Find any polygonal line whose sharpness is $\leq c$.
• Given an integer $c$.
  Answer $q$ queries, each specified by a single integer $k_i$ ($c \leq k_i \leq n - c$). In the $i$-th query, you need to construct a polygonal line that has sharpness exactly $k_i$.
• Given an integer $c$.
  For each $k$ from $c$ to $n - c$, construct a polygonal line $p^{(k)}$ with sharpness exactly $k$. Provide $n - 2c + 1$ numbers $\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)$ as the answer, where $hash(p) = \left( \sum\limits_{i=1}^{n} p_i b^{i-1} \right) \bmod m$ is the polynomial hash of permutation $p$ with parameters $b = 10^6 + 3$ and $m = 10^9 + 7$.
  Then answer $q$ queries, each specified by a single integer $k_i$ ($c \leq k_i \leq n - c$). In the $i$-th query, you need to provide the polygonal line $p^{(k_i)}$. It will be checked that the sharpness of this polygonal line is exactly $k_i$ and its hash matches the previously provided value $\text{hash}\left(p^{(k_i)}\right)$.
  Note that queries will appear after receiving the hashes.

It is guaranteed, that under given constraints, the answers always exist.

Interaction Protocol

The first line contains two integers $\text{task}$, $\text{group}$ ($1 \leq \text{task} \leq 4$, $0 \leq \text{group} \leq 21$) --- the number of the task to be solved in this test and the test group number.

The second line contains a single integer $n$ ($3 \leq n \leq 80\,000$) --- the number of points on the plane.

Each of the next $n$ lines contains two integers $x_i$, $y_i$ ($|x_i|, |y_i| \leq 10^9$) --- the coordinates of the points. It is guaranteed that all $x_i$ are distinct and all $y_i$ are distinct.

If $\text{task} = 1$, then the input ends here and you should output any permutation with the maximum possible sharpness. The interaction ends here.

If $\text{task} \neq 1$, then the next line contains a single integer $c$ ($2 \leq c \leq \frac{n}{2}$).

If $\text{task} = 2$, then the input ends here and you should output any permutation with sharpness $\leq c$. The interaction ends here.

If $\text{task} = 4$, your solution should output $n - 2c + 1$ integers $\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)$, where $0 \leq \text{hash}\left(p^{(i)}\right) < 10^9 + 7$. Note that this should not be done if $\text{task} = 3$.

Further interaction occurs only if $\text{task} = 3$ or $\text{task} = 4$.

The next line contains a single integer $q$ ($1 \leq q \leq 50$) --- the number of queries.

Then $q$ times, in each line, a query $k_i$ ($c \leq k_i \leq n - c$) appears. As a response, you should output a permutation on a separate line. The sharpness of this permutation should be exactly $k_i$. If $\text{task} = 4$, the hash of this permutation should match the previously provided hash.

Since this is an interactive problem, after outputting each line, do not forget to output a newline character and flush the output buffer.

1 0
4
2 3
1 8
4 2
0 0

3 2 4 1

2 0
5
-2 0
-1 -1
0 1
2 -2
3 -3
2

5 4 3 1 2

3 0
6
0 0
1 1
2 2
3 -3
4 -2
5 -1
2
3
2

3

4

1 2 3 4 5 6

4 5 6 1 3 2

6 2 4 3 5 1

4 0
5
-2 -1
-1 1
1 6
0 -3
2 0
2

2
2

3

534735187 776162084


4 5 1 2 3

1 3 2 5 4

提示

Note

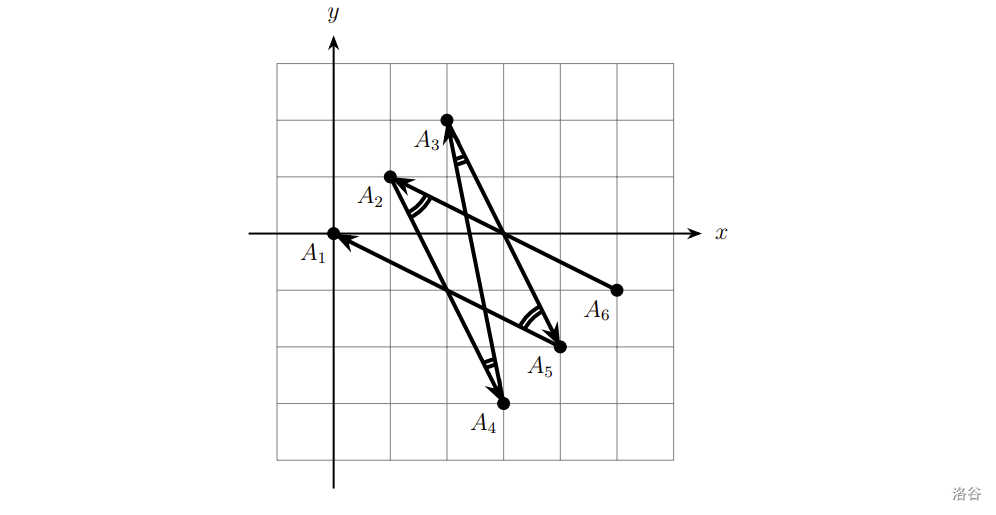
In all the figures, acute angles are denoted by two arcs, and non-acute angles are denoted by a single arc.

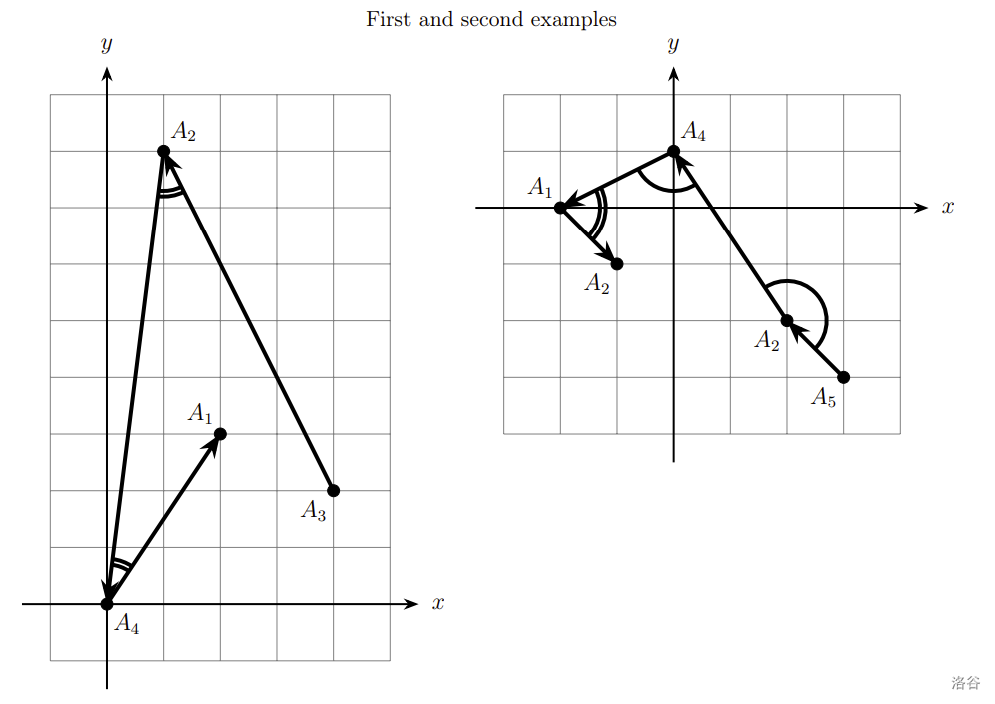
In the first example all angles are sharp, so the line has maximum sharpness $2$.

In the second sample the sharpness equals to $1$, it is $\leq 2$.

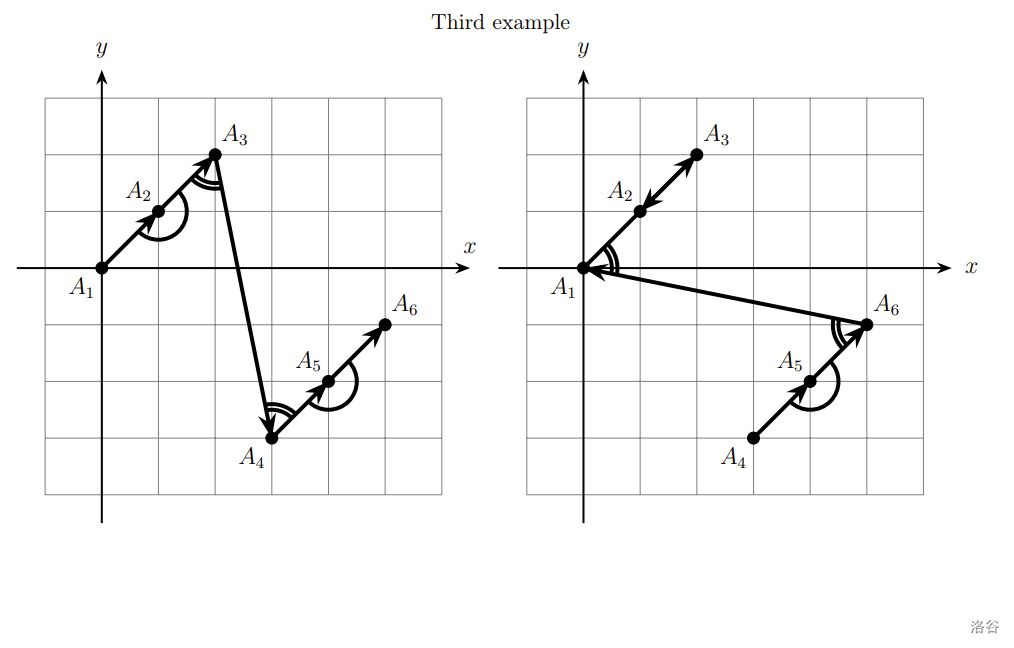
In the third example the lines have sharpness $2$, $3$, $4$.

In the forth example we build lines that have sharpness $2$ and $3$. The lines have hashes equal to the ones provided earlier.

Scoring

The tests for this problem consist of twenty-one groups. Points for each group are given only if all tests of the group and all tests of the required groups are passed.

Group	Points	task	$n$	$c$	Additional constraints	Required Groups	Comment
0		-		-	-	-	Examples.
1	8	1	$n \leq 20000$		$x_i < x_{i+1}, y_i < y_{i+1}$
2	6		$n \leq 10$		random points
3	5		$n \leq 1000$			2
4			$n \leq 20000$			2 - 3
5	6				-	1 - 4
6	17	2	$n = 80000$	$c = 800$		-
7		3			$x_i < x_{i+1}, y_i < y_{i+1}$
8	4		$n = 50$	$c = 25$	random points
9			$n = 200$	$c = 80$
10			$n = 1000$	$c = 300$
11	3		$n = 5000$	$c = 600$
12			$n = 80000$	$c = 35000$
13				$c = 5000$		12
14				$c = 2000$	-	12 - 13
15	2			$c = 800$		7, 12 - 14
16	6	4			$x_i < x_{i+1}, y_i < y_{i+1}$	-
17	3		$n = 5000$	$c = 600$	random points
18			$n = 80000$	$c = 35000$
19				$c = 5000$		18
20				$c = 2000$	-	18 - 19
21	2			$c = 800$		16, 18 - 20

In the groups where it is indicated that the points are random, all coordinates of all points $x_i$, $y_i$ are randomly generated with equal probability in the interval $[-10^9, 10^9]$.