题目描述

Given a vertex-colored tree with $\mathrm{N}$ nodes, can it be drawn in a 2D plane with a line of symmetry?

Formally, a tree is line-symmetric if each vertex can be assigned a location in the 2D plane such that:

• All locations are distinct.
• If vertex $\mathbf{v}_{\mathrm{i}}$ has color $\mathbf{C}$ and coordinates $\left(\mathrm{x}_{\mathrm{i}}, \mathrm{y}_{\mathrm{i}}\right)$, there must also be a vertex $\mathbf{v}_{\mathrm{i}}^{\prime}$ of color $\mathbf{C}$ located at $\left(-\mathrm{x}_{\mathrm{i}}, \mathrm{y}_{\mathrm{i}}\right)$ -- Note if $\mathrm{x}_{\mathrm{i}}$ is 0, $\mathbf{v}_{\mathrm{i}}$ and $\mathbf{v}_{\mathrm{i}}^{\prime}$ are the same vertex.
• For each edge $\left(\mathbf{v}_{\mathrm{i}}, \mathbf{v}_{\mathrm{j}}\right)$, there must also exist an edge $\left(\mathbf{v}_{\mathrm{i}}^{\prime}, \mathbf{v}_{\mathrm{j}}^{\prime}\right)$.
• If edges were represented by straight lines between their end vertices, no two edges would share any points except where adjacent edges touch at their endpoints.

输入格式

The first line of the input gives the number of test cases, $\mathrm{T}$. $\mathrm{T}$ test cases follow.

Each test case starts with a line containing a single integer $\mathrm{N}$, the number of vertices in the tree.

$\mathrm{N}$ lines then follow, each containing a single uppercase letter. The $\mathrm{i}$-th line represents the color of the $\mathrm{i}$-th node.

$\mathrm{N}-1$ lines then follow, each line containing two integers $\mathrm{i}$ and $\mathrm{j}(1 \leq \mathrm{i}<\mathrm{j} \leq \mathrm{N})$. This denotes that the tree has an edge from the $\mathrm{i}$-th vertex to the $\mathrm{j}$-th vertex. The edges will describe a connected tree.

输出格式

For each test case, output one line containing "Case #x: y", where $\mathrm{x}$ is the case number (starting from 1) and $\mathrm{y}$ is "SYMMETRIC" if the tree is line-symmetric by the definition above or "NOT SYMMETRIC" if it isn't.

3
4
R
G
B
B
1 2
2 3
2 4
4
R
G
B
Y
1 2
2 3
2 4
12
Y
B
Y
G
R
G
Y
Y
B
B
B
R
1 3
1 9
1 10
2 3
3 7
3 8
3 11
4 8
5 7
6 7
8 12

Case #1: SYMMETRIC
Case #2: NOT SYMMETRIC
Case #3: SYMMETRIC

提示

Sample Explanation

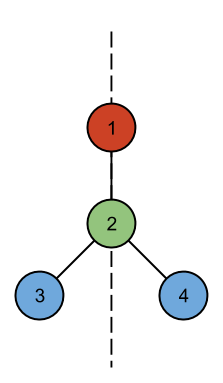
The first case can be drawn as follows:

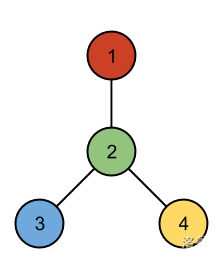
No arrangement of the second case has a line of symmetry:

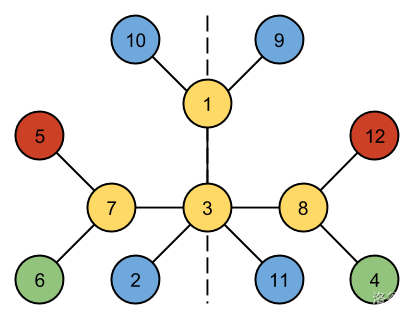
One way of drawing the third case with a symmetry line is as follows:

Limits

• $1 \leq T \leq 100$

Small dataset(7 Pts)

• Time Limit: 60 3 seconds
• $2 \leq N \leq 12$

Large dataset(18 Pts)

• Time Limit: 120 5 seconds
• $2 \leq N \leq 10000$