题目描述

Your task in this problem is to find out the minimum number of stones needed to place on an $N$-by-$M$ rectangular grid ($N$ horizontal line segments and $M$ vertical line segments) to enclose at least $K$ intersection points. An intersection point is enclosed if either of the following conditions is true:

1. A stone is placed at the point.
2. Starting from the point, we cannot trace a path along grid lines to reach an empty point on the grid border through empty intersection points only.

For example, to enclose $8$ points on a $4\times 5$ grid, we need at least $6$ stones. One of many valid stone layouts is shown below. Enclosed points are marked with an "x".

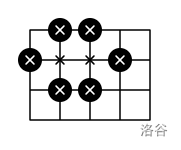
输入格式

The first line of the input gives the number of test cases, $T$. $T$ lines follow. Each test case is a line of three integers: $N$ $M$ $K$.

输出格式

For each test case, output one line containing "Case #$x$: $y$", where $x$ is the test case number (starting from 1) and $y$ is the minimum number of stones needed.

2
4 5 8
3 5 11

Case #1: 6
Case #2: 8

提示

Sample Explanation

• $1 \leq T \leq 100$.
• $1 \leq N$.
• $1 \leq M$.
• $1 \leq K \leq N \times M$.

Small dataset(15 Pts)

• Time limit: 60 3 seconds.
• $N \times M \leq 20$.

Large dataset(30 Pts)

• Time limit: 120 10 seconds.
• $N \times M \leq 1000$.