题目描述

You are a landlord who owns a building that is an $R \times C$ grid of apartments; each apartment is a unit square cell with four walls. You want to rent out $N$ of these apartments to tenants, with exactly one tenant per apartment, and leave the others empty. Unfortunately, all of your potential tenants are noisy, so whenever any two occupied apartments share a wall (and not just a corner), this will add one point of unhappiness to the building. For example, a $2 \times 2$ building in which every apartment is occupied has four walls that are shared by neighboring tenants, and so the building's unhappiness score is $4$.

If you place your $N$ tenants optimally, what is the minimum unhappiness value for your building?

输入格式

The first line of the input gives the number of test cases, $T$. $T$ lines follow; each contains three space-separated integers: $R$, $C$, and $N$.

输出格式

For each test case, output one line containing "Case #$x$: $y$", where $x$ is the test case number (starting from $1$) and $y$ is the minimum possible unhappiness for the building.

4
2 3 6
4 1 2
3 3 8
5 2 0

Case #1: 7
Case #2: 0
Case #3: 8
Case #4: 0

提示

Sample Explanation

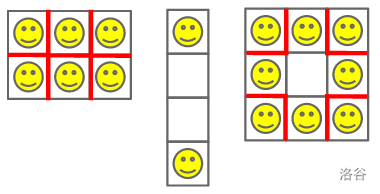
In Case #1, every room is occupied by a tenant and all seven internal walls have tenants on either side.

In Case #2, there are various ways to place the two tenants so that they do not share a wall. One is illustrated below.

In Case #3, the optimal strategy is to place the eight tenants in a ring, leaving the middle apartment unoccupied.

Here are illustrations of sample cases 1-3. Each red wall adds a point of unhappiness.

Sample Explanation

• $1 \leq T \leq 1000$.
• $0 \leq N \leq R \times C$.

Small dataset(12 Pts)

• Time limit: 240 5 seconds.
• $1 \leq R \times C \leq 16$.

Large dataset(15 Pts)

• Time limit: 480 10 seconds.
• $1 \leq R \times C \leq 10000$.