题目描述

An $N$-omino is a two-dimensional shape formed by joining $N$ unit cells fully along their edges in some way. More formally, a 1-omino is a $1\times 1$ unit square, and an $N$-omino is an $(N-1)$-omino with one or more of its edges joined to an adjacent $1\times 1$ unit square. For the purpose of this problem, we consider two $N$-ominoes to be the same if one can be transformed into the other via reflection and/or rotation. For example, these are the five possible $4$-ominoes:

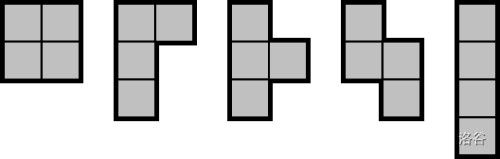
And here are some of the $108$ possible $7$-ominoes:

Richard and Gabriel are going to play a game with the following rules, for some predetermined values of $\mathbf{X}$, $\mathbf{R}$, and $\mathbf{C}$:

1. Richard will choose any one of the possible $\mathbf{X}$-ominoes.
2. Gabriel must use at least one copy of that $\mathbf{X}$-omino, along with arbitrarily many copies of any $\mathbf{X}$-ominoes (which can include the one Richard chose), to completely fill in an $\mathbf{R}$-by-$\mathbf{C}$ grid, with no overlaps and no spillover. That is, every cell must be covered by exactly one of the $\mathbf{X}$ cells making up an $\mathbf{X}$-omino, and no $\mathbf{X}$-omino can extend outside the grid. Gabriel is allowed to rotate or reflect as many of the $\mathbf{X}$-ominoes as he wants, including the one Richard chose. If Gabriel can completely fill in the grid, he wins; otherwise, Richard wins.

Given particular values $\mathbf{X}$, $\mathbf{R}$, and $\mathbf{C}$, can Richard choose an $\mathbf{X}$-omino that will ensure that he wins, or is Gabriel guaranteed to win no matter what Richard chooses?

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ lines follow. Each contains three space-separated integers: $\mathbf{X}$, $\mathbf{R}$, and $\mathbf{C}$.

输出格式

For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is either RICHARD (if there is at least one choice that ensures victory for Richard) or GABRIEL (if Gabriel will win no matter what Richard chooses).

4
2 2 2
2 1 3
4 4 1
3 2 3

Case #1: GABRIEL
Case #2: RICHARD
Case #3: RICHARD
Case #4: GABRIEL

提示

Sample Explanation

In case #1, Richard only has one $2$-omino available to choose -- the $1\times 2$ block formed by joining two unit cells together. No matter how Gabriel places this block in the $2\times 2$ grid, he will leave a hole that can be exactly filled with another $1\times 2$ block. So Gabriel wins.

In case #2, Richard has to choose the $1\times 2$ block, but no matter where Gabriel puts it, he will be left with a single $1\times 1$ hole that he cannot fill using only $2$-ominoes. So Richard wins.

In case #3, one winning strategy for Richard is to choose the $2\times 2$ square $4$-omino. There is no way for Gabriel to fit that square into the $4\times 1$ grid such that it is completely contained within the grid, so Richard wins.

In case #4, Richard can either pick the straight $3$-omino or the L-shaped $3$-omino. In either case, Gabriel can fit it into the grid and then use another copy of the same $3$-omino to fill in the remaining hole.

Limits

Small dataset(8 Pts)

• Time limit: 240 5 seconds.
• $\mathbf{T} = 64$.
• $1 \leq \mathbf{X}, \mathbf{R}, \mathbf{C} \leq 4$.

Large dataset(26 Pts)

• Time limit: 480 10 seconds.
• $1 \leq \mathbf{T} \leq 100$.
• $1 \leq \mathbf{X}, \mathbf{R}, \mathbf{C} \leq 20$.