题目描述

You are an employee of the Fence Construction Company and have been tasked with the construction of $F$ fences. Each fence runs in a straight line from one point to another. Formally, each fence is a segment connecting two different points in two-dimensional space. Fences do not intersect each other, except possibly at their endpoints. The fences are all connected, that is, for any pair of fences $f$ and $g$ there exists a path $f = f_1, f_2, \dots, f_k = g$ such that $f_i$ shares an endpoint with $f_{i+1}$.

At the time you begin your work, no fences have been built. Construction is done using a special fence-shooting 3D printer. There is only one such device, so fences are built one at a time. The printer is small enough that you can consider it a single point on the plane.

To build a fence $f$, you must first position the printer at a point $p$ in the plane such that the printer can see all of $f$ without being obstructed by previously constructed fences. Formally, $p$ has to be such that:

• $p$ is not on $f$ (not even at an endpoint).
• for any point $q$ on $f$ that is not an endpoint of $f$, the segment connecting $p$ and $q$ does not intersect any previously built fence.

To position the printer, you can move it from its current position in a contiguous and not necessarily straight line through the plane, as long as the line does not intersect any previously built fences (not even at an endpoint). You can choose any position for the printer to be at before the first fence is built and after the last fence is built.

Having to follow this procedure means that you cannot necessarily build the fences in any order. For example, you might choose an order that blocks off the printer and prevents you from moving it to where it needs to be.

The director of the organization has drafted a relative ordering involving $K$ of the fences (but none of these have been built yet) without giving much thought to it. To avoid angering them, you need to use this ordering, inserting the remaining $F-K$ fences anywhere you like to complete the ordering.

Given these restrictions, find an order in which to build the fences. It is guaranteed that at least one valid order exists.

输入格式

The first line of the input gives the number of test cases, $T$. $T$ test cases follow. Each begins with one line containing two integers $F$ and $K$: the total number of fences and the number of fences in the director's incomplete ordering. Then, $F$ more lines follow; the $i$-th of these lines (counting starting from 1) contains four integers $A_i$, $B_i$, $C_i$ and $D_i$, indicating that the $i$-th fence is a line segment from $(A_i, B_i)$ to $(C_i, D_i)$. The first $K$ fences given in the input are the $K$ fences in the director's ordering.

输出格式

For each test case, output one line beginning Case #x: y, where $x$ is the test case number (starting from 1), and $y$ is a space-separated ordering of the integers between 1 and $F$, inclusive, giving a valid order in which to build the fences.

3
6 2
0 0 7 7
15 -2 10 0
0 0 0 10
0 0 10 0
0 10 10 10
10 0 10 10
6 1
0 0 0 10
0 0 10 0
0 10 10 10
10 0 10 10
0 0 7 7
15 -2 10 0
11 4
-10 0 10 0
-10 0 0 10
10 0 0 10
0 2 0 5
0 2 10 0
10 0 0 5
15 3 18 3
15 3 15 9
18 3 15 9
15 3 16 5
0 10 15 3

Case #1: 1 2 3 4 5 6
Case #2: 5 6 1 2 3 4
Case #3: 11 10 7 8 9 1 2 3 6 5 4

提示

Sample Explanation

Note that the last sample case would not appear in test set $1$.

In Sample Case #1, it is possible to build the fences in the order they are given: $1, 2, 3, 4, 5, 6$. Note that fence $1$ must come earlier in the order than fence $2$, per the director's list.

In Sample Case #2, it is not possible to build the fences in the given order! One possible order is: $5, 6, 1, 2, 3, 4$. Note that when the director's list includes only one fence, the relative order condition is always trivially satisfied.

In Sample Case #3, it is possible to build the fences in the order: $11, 10, 7, 8, 9, 1, 2, 3, 6, 5, 4$. Note that fences $1, 2, 3$ and $4$ must be built in that relative order.

The following pictures illustrate one valid way of building the fences for Sample Case #1.

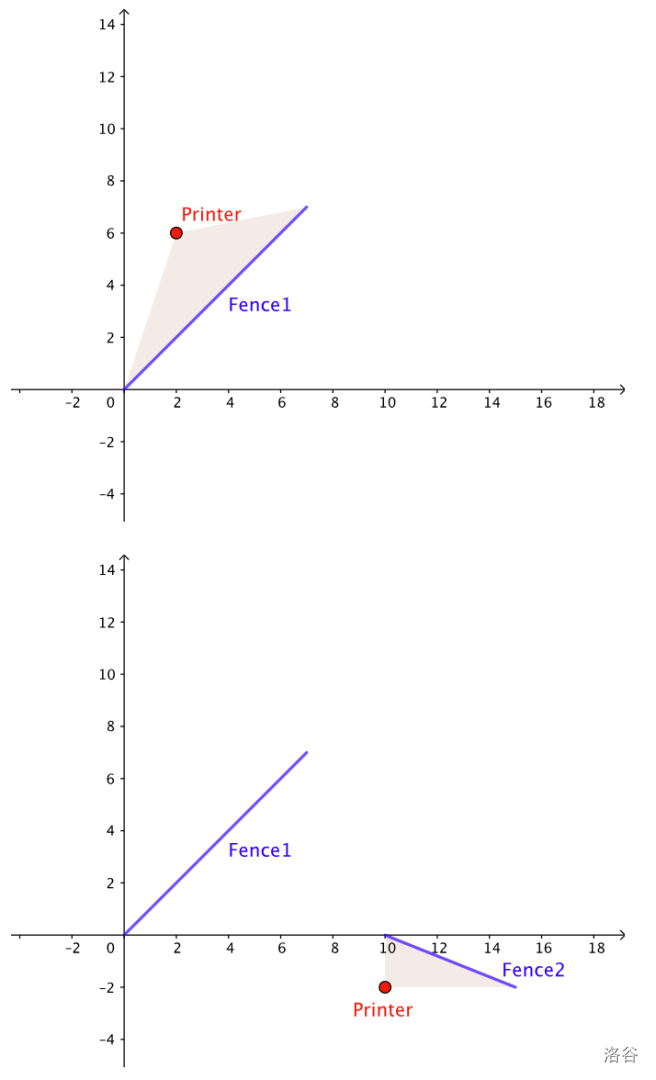
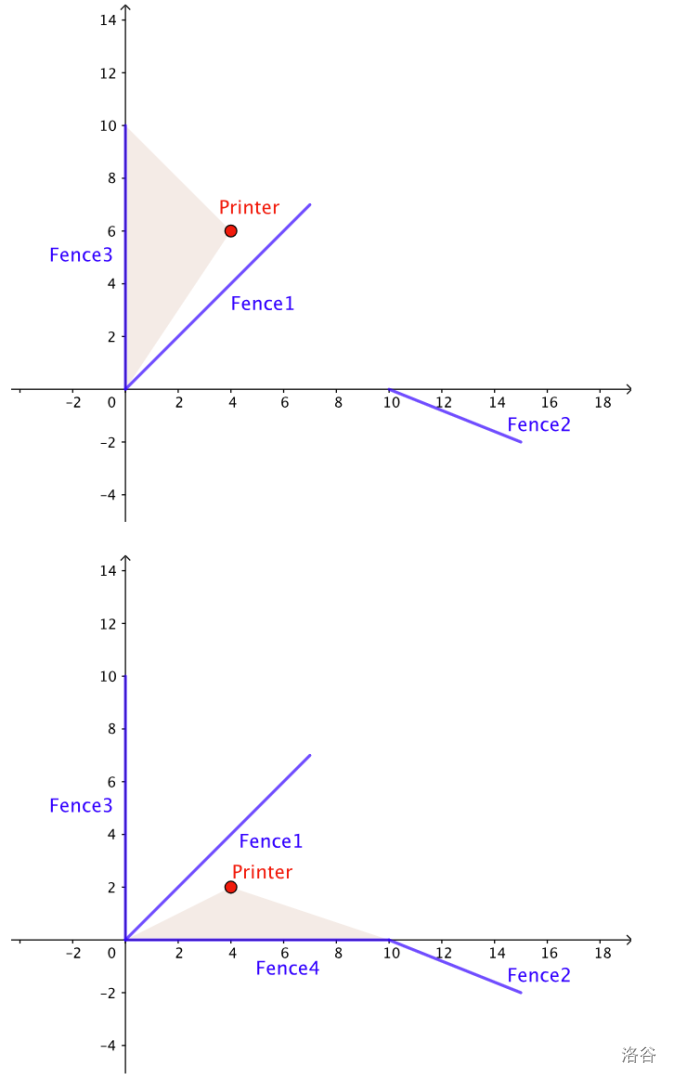
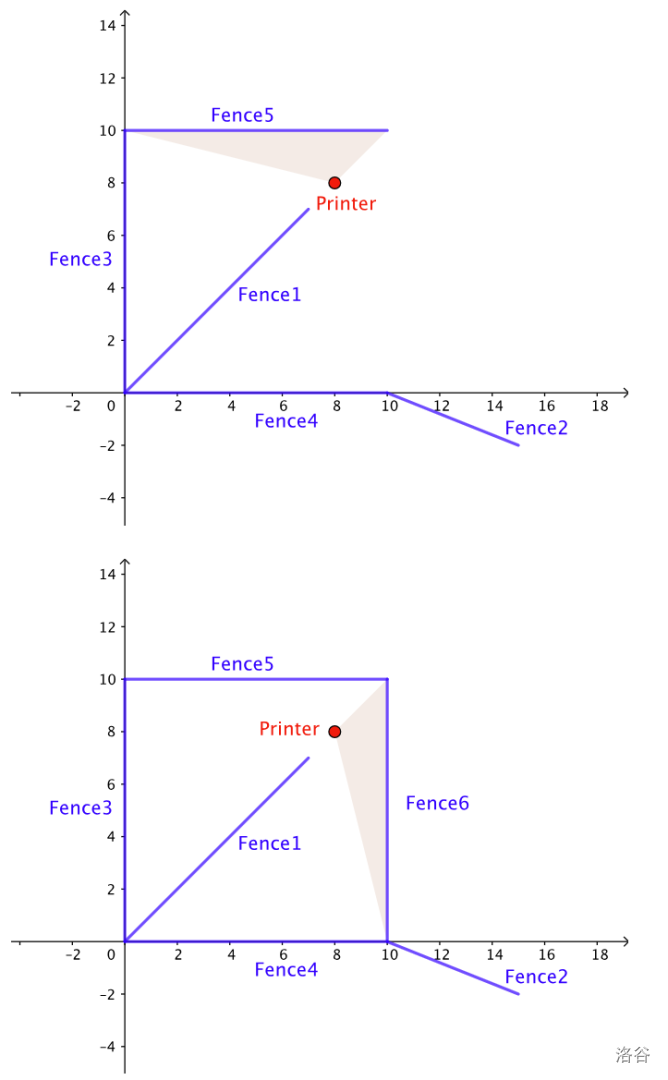
Limits

• $1 \leq T \leq 100$.
• $4 \leq F \leq 300$.
• $-10^5 \leq A_i \leq 10^5$, for all $i$.
• $-10^5 \leq B_i \leq 10^5$, for all $i$.
• $-10^5 \leq C_i \leq 10^5$, for all $i$.
• $-10^5 \leq D_i \leq 10^5$, for all $i$.
• $(A_i, B_i) \neq (C_i, D_i)$, for all $i$.
• If $p$ is a non-endpoint point on a fence, then $p$ is not a point of any other fence.
• The given fences are connected, as defined in the statement.
• There is at least one ordering of the fences that satisfies all the construction restrictions in the statement.

Test set 1 (12 Pts, Visible)

• $1 \leq K \leq 2$.

Test set 2 (23 Pts, Hidden)

• $1 \leq K < F$.