题目描述

Anthropologists have learned something surprising about a certain ancient Greek society of geometers: they loved partying as much as they loved mathematics! In fact, they kept hosting larger and larger parties over the years, so they needed to raise the roof of their ballroom to keep the noise level tolerable.

We know that the roof of their ballroom was always supported by the tips of exactly three columns; these columns were infinitely thin line segments that originated on the floor and rose up perpendicular to the floor. Whenever the society wanted to raise the roof, they would begin by removing the existing roof. Then, they would build a new column in a location where there was not already a column. Finally, they would rest a new roof on the tips of the new column and the two most recently built of the previously existing columns. For mystical reasons, no three column bases were ever collinear, and no four column tips were ever coplanar.

Each roof was a convex polygon that was part of the plane defined by the three tips that supported it. For each column $c$ built before the supporting ones, the roof did not intersect $c$ at any point and was large enough to cover the space above $c$. The roof did not touch the floor. The different roofs did not necessarily all have the same shape.

On an archeological dig, you found all $N$ columns that the society ever built, but no roof. You want to determine a possible order in which the columns could have been built that is consistent with the rules above. A possible order is an ordering of the $N$ columns such that, for each prefix of length at least 4 of the ordering, there is a roof (convex polygon) that contains the tips of the last three columns in the prefix, and for each other column in the prefix with a tip at $(x, y, h)$ the roof contains a point $(x, y, z)$ with $z > h$.

输入格式

The first line of the input gives the number of test cases, $T$. $T$ test cases follow. Each test case begins with one line containing an integer $N$: the number of columns. Then, $N$ more lines follow; the $i$-th of these lines contains three integers $X_i$, $Y_i$, and $H_i$, representing the $X$ and $Y$ coordinates and height above the ground of the tip of the $i$-th column.

输出格式

For each test case, output one line containing Case #x: y1 y2 ... yN, where $x$ is the test case number (starting from 1), and each $y_i$ is a different integer between 1 through $N$. These represent a possible ordering of the columns, with $y_i$ being the index in the input of the $i$-th built column.

It is guaranteed that at least one valid answer always exists. If there are multiple possible answers, you may output any of them.

3
5
-1 0 3
1 2 4
1 -2 4
3 1 3
3 -1 2
4
1 1 1
2 2 3
2 3 4
10 11 120
4
1 1 1
2 2 3
2 3 4
10 11 12

Case #1: 5 4 3 1 2
Case #2: 3 2 1 4
Case #3: 1 2 4 3

提示

Sample Explanation

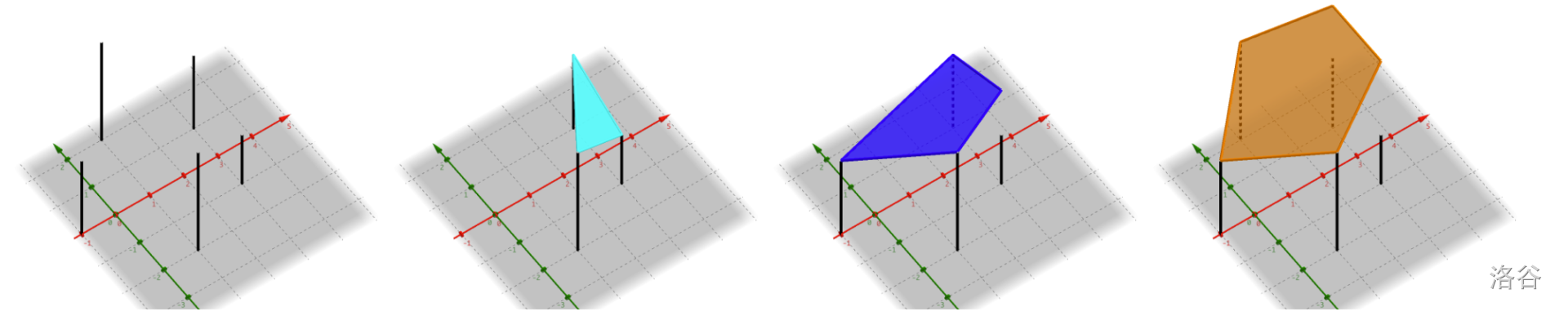
The following pictures illustrate Sample Case #1.

Limits

• $1 \leq T \leq 100$.
• $-10^6 \leq X_i \leq 10^6$, for all $i$.
• $-10^6 \leq Y_i \leq 10^6$, for all $i$.
• $1 \leq H_i \leq 10^6$, for all $i$.
• $(X_i, Y_i)$, $(X_j, Y_j)$, and $(X_k, Y_k)$ are not collinear, for all distinct $i, j, k$.
• $(X_i, Y_i, H_i)$, $(X_j, Y_j, H_j)$, $(X_k, Y_k, H_k)$, and $(X_l, Y_l, H_l)$ are not coplanar, for all distinct $i, j, k, l$.

Test set 1 (7 Pts, Visible)

• $4 \leq N \leq 10$.

Test set 2 (19 Pts, Hidden)

• $4 \leq N \leq 1000$.