题目描述

A certain toy consists of a grid of 2 or more columns and 1 or more rows, where each cell of the grid contains either a $\backslash$ ramp or a $/$ ramp, or is empty. The leftmost and rightmost columns are empty and the bottom row is also empty. Balls are dropped into the top row and fall vertically, sliding on ramps. To prevent balls from getting stuck, a cell with a $\backslash$ ramp is never immediately to the left of a cell with a $/$ ramp.

When a ball is dropped into the top row, it moves deterministically as follows:

• A ball in an empty cell moves to the cell immediately below its current cell, unless it is in the bottom row, in which case it does not move any more.
• A ball in a cell containing a $\backslash$ ramp moves to the cell immediately below and to the right of its current cell.
• A ball in a cell containing a $/$ ramp moves to the cell immediately below and to the left of its current cell.

To see the mechanism to its full extent, the user drops exactly one ball into each column. Balls do not interfere with each other, and it is possible for a cell to contain multiple balls.

Your friend has a toy with $C$ columns and an unknown number of rows. They just dropped one ball into the top row of each column, and waited for all balls to stop moving. Then, they counted how many balls ended up in each of the cells of the bottom row, and gave you those results... but you think it is possible that they made a mistake. Can you create a layout that is consistent with the results and uses as few rows as possible, or determine that no such layout exists?

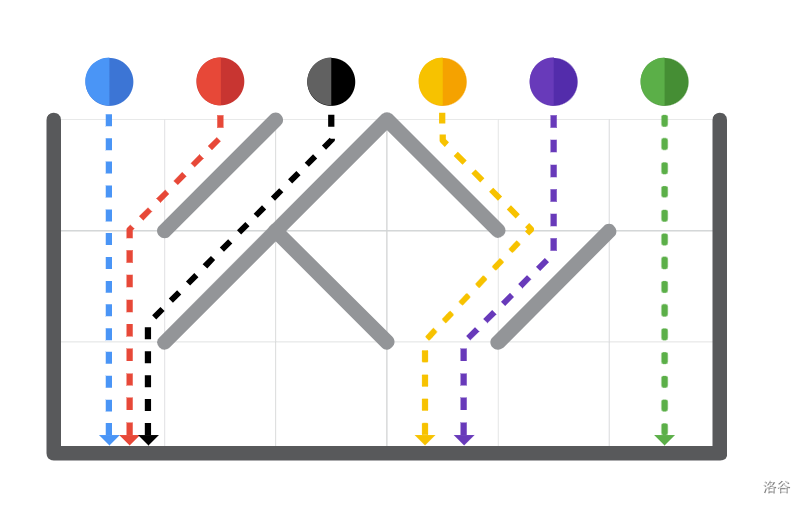
For example, if your friend reported the values $3 \ 0 \ 0 \ 2 \ 0 \ 1$, one possible solution would be the following. (Note that it is not necessary to use a minimal number of ramps, or for every ramp to affect the balls.)

./\\...
./\.\/.
.......

Here are the paths that the balls would take when falling through that grid:

输入格式

The first line of the input gives the number of test cases, $T$. $T$ test cases follow. Each begins with one line containing an integer $C$: the number of columns in your friend's falling ball toy. Then, there is one more line containing $C$ integers $B_i$. The i-th of these integers represents the number of balls that ended up in the i-th cell from the left of the bottom row of your friend's falling ball toy, according to the data they gave you.

输出格式

For each test case, output one line containing Case #x: y, where $x$ is the test case number (starting from 1) and $y$ is either IMPOSSIBLE, or the number of rows in your layout, as described above. If $y$ is not IMPOSSIBLE, output $y$ more rows, representing the rows of your proposed falling ball toy layout, in order from top to bottom. Use . to represent a cell with no ramp, and $\backslash$ or $/$ to represent the ramps. The layout must obey all of the rules in the problem statement.

3
4
1 1 1 1
3
0 2 1
6
3 0 0 2 0 1

Case #1: 1
....
Case #2: IMPOSSIBLE
Case #3: 3
.//\..
./\./.
......

提示

Sample Explanation

Note that the last sample case would not appear in Test set 1.

The following layout is the only valid solution for Sample Case #1. (There must be at least one row, and including any more rows would make the solution use more rows than needed. It is not legal to include any ramps in the bottom row.)

....

In Sample Case #2, there is no way to prevent the leftmost ball from falling to the bottom of its column without adding a ramp, but ramps cannot be added to that column.

Sample Case #3 is the one described at the end of the problem statement. Note that the following invalid layout for Sample Case #3 breaks several rules: it has more rows than needed, it has ramps in the three illegal zones (left column, right column, bottom row), and it contains a $\backslash$ ramp immediately to the left of a $/$ ramp.

\\..\/
../.\/
./../.
..../.

Limits

• $1 \leq T \leq 100$.
• $0 \leq B_i \leq C$, for all $i$.
• The sum (over all $i$ from 1 to $C$, inclusive) of all $B_i$ values = $C$.

Test set 1 (5 Pts, Visible)

• $2 \leq C \leq 5$.

Test set 2 (12 Pts, Hidden)

• $2 \leq C \leq 100$.